Testing for ion-mediated enhancement of the hydraulic conductance of the leaf xylem in diverse angiosperms
Abstract
Replacing ultra-pure water solution with ion solution closer to the composition of natural xylem sap increases stem hydraulic conductance by up to 58%, likely due to changes in electroviscosity in the pit membrane pores. This effect has been proposed to contribute to the control of plant hydraulic and stomatal conductance and potentially to influence on carbon balance during dehydration. However, this effect has never been directly tested for leaf xylem, which constitutes a major bottleneck in the whole plant. We tested for an ion-mediated increase in the hydraulic conductance of the leaf xylem (Kx) for seven species diverse in phylogeny and drought tolerance. Across species, no significant changes in Kx were observed between 0 and 15 mM KCl. We further tested for an effect of ion solution during measurements of Kx vulnerability to dehydration in Quercus agrifolia and found no significant impact. These results for leaf xylem contrast with the often strong ion effect reported for stems, and we suggest several hypotheses to account for the difference, relating to the structure of xylem conduits across vein orders, and the ultrastructure of leaf xylem pores. A negligible ion response in leaves would weaken xylem sap ion-mediated control of plant hydraulic conductance, facilitating modeling of whole plant hydraulic behavior and its influence on productivity.
Introduction
In the last fifty years, lab techniques to measure hydraulic conductance of plant organs have revolutionized the understanding of water relations and allied fields (Sack et al., 2016). These hydraulics measurements have enabled a new understanding of the physics of water movement through trees (Tyree and Zimmermann, 2002), and provided key measures of vulnerability to drought (Choat et al., 2012). Several discoveries revealed that the hydraulic system was surprisingly dynamic. For example, changes in hydraulic conductance due to external stimuli such as light and temperature and internal effects such as sap ion concentration highlighted the possibility of rapid xylem responses that would importantly impact on the whole plant (e.g., Tyree and Zimmermann, 2002; Sack and Tyree, 2005; Nardini et al., 2011). The ion-mediated response, discovered in stems (Zimmermann, 1978; van Ieperen et al., 2000; Zwieniecki et al., 2001) held particular promise as an important modulator of plant hydraulic conductance over the course of a day, and for maintaining photosynthesis during drought (Nardini et al., 2011). If such a response were to influence the whole plant hydraulic system, it would need to be considered in models of plant water transport and its influence on productivity.
Yet, as the importance of hydraulics measurements became clearer, so did the realization that lab experiments on such a complex system can be prone to artefacts (Rockwell et al., 2014). As such, the field of hydraulics has grown extremely rigorous and attentive to possible measurement artefacts, and techniques are constantly improving. Some artefacts found for stems do not apply to leaves. For example, methods for measuring stem hydraulic conductance of long vesseled-species such as oak or lianas are prone to open vessel artefacts (Cochard et al., 2013), but hydraulics measurements on leaves consider flow through the entire organ and are not subject to open vessel artefacts. Further, for stems, cutting segments under water without first releasing tension can induce artefactual embolism (Wheeler et al., 2013), though such a cutting artefact was not found in leaves (Scoffoni and Sack, 2015). However, the measurement artifacts caused by the use of pure water instead of natural sap (which is enriched in ions) seen in stems might also hold for leaves, though this has never been rigorously tested. While early measurements of stem hydraulic conductance often utilized pure water, it is now common practice to use KCl solutions when measuring stem hydraulic conductance, given that the ionic composition of the stem xylem sap can enhance stem hydraulic conductance in some species (Zwieniecki et al., 2001; Jansen et al., 2011), possibly through changes in electroviscosity within the pit pores of xylem conduits (Jansen et al., 2011; Santiago et al., 2013). Only two angiosperm species to our knowledge have been tested and these showed no ion effect on whole leaf hydraulic conductance (Kleaf) (Sack et al., 2004). However, no studies to our knowledge have directly tested for such effect on the leaf xylem hydraulic conductance (Kx). This process could impact Kleaf, and thereby the whole plant, depending on both the partitioning of resistances inside and outside the xylem, which can be highly variable across species (Sack and Holbrook, 2006; Scoffoni et al., 2016), and the magnitude of the potential ion-mediated enhancement of Kx.
The aim of our study was to test for an ion-mediated enhancement of leaf xylem hydraulic conductance (Kx) across seven diverse angiosperm species in phylogeny. For one species, we further tested whether using an ion solution instead of pure water would influence the measurement of Kx in dehydrated leaves. An effect of ion concentration on the hydraulic conductance through the leaf xylem across diverse species would have consequences for (1) our ability to generalize from methodologies applied thus far for measuring Kx and Kleaf, and (2) the modeling of leaf and whole plant hydraulic conductance, given that a dynamic response in leaf xylem could impact whole plant hydraulic behavior.
Material and Methods
Species and sampling approach
Experiments focused on seven species growing in and around the campus of the University of California, Los Angeles and Will Rogers State Park: Cercocarpus betuloides, Comarostaphylis diversifolia, Lantana camara, Magnolia grandiflora, Malosma laurina, Platanus racemosa and Quercus agrifolia. These species were selected for diversity in phylogeny and drought tolerance (Table 1). Sun exposed shoots were sampled January to November of 2014 and placed in plastic bags filled with wet paper towels. Shoots were immediately brought back to the lab, and two nodes were cut off each shoot under water. Then, shoots were left to rehydrate at least 12h overnight in deionized water and covered with dark plastic bags filled with wet paper towels.
Testing the ion effect on maximum leaf xylem hydraulic conductance
We tested for an ion enhancement of leaf xylem hydraulic conductance by measuring Kx using the vacuum pump method, as described in previous studies (Scoffoni and Sack, 2015; Scoffoni et al., 2017b) in which the flow rate of water through the petiole and vein xylem is measured at different vacuum levels, and Kx is calculated as the slope of flow rate against vacuum level (Figure 1).
Figure 1. Using the vacuum pump method to measure leaf xylem hydraulic conductance (Kx). Shoots were dehydrated to given water potentials, then one leaf (still attached to the shoot) was placed under the perfusing solution (0 or 15 mM KCl) and over a light bench, and minor veins were severed between approximately 95% of tertiary veins throughout the leaf using a scalpel (only a tiny fraction of the actual cuts made are depicted in the image). The leaf was then cut off the shoot under water and rapidly connected by tubing to a water source on a balance. The leaf was then placed in a vacuum chamber. The flow rate of water movement through the petiole and leaf xylem was measured at five different vacuum levels. Kx was calculated as the slope of flow rate over vacuum pressures, and further normalized by leaf temperature and leaf area.
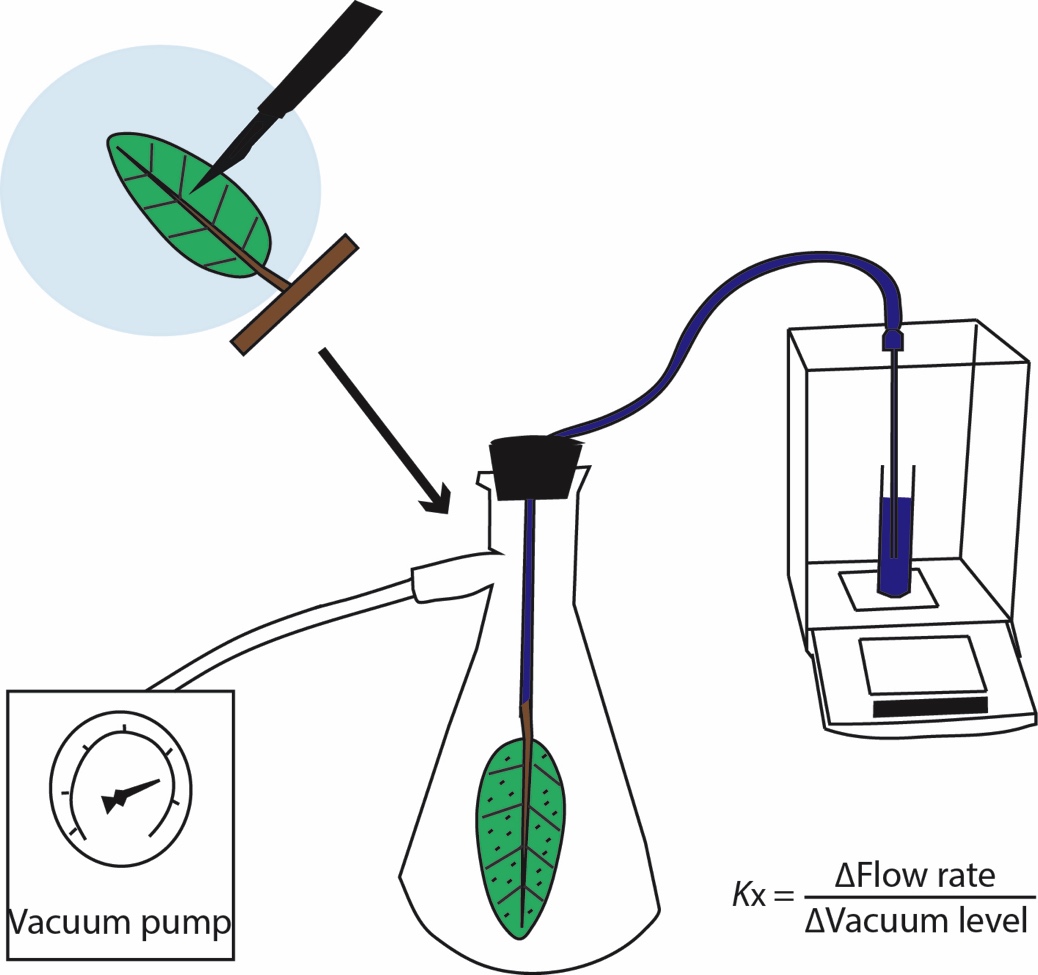
In the vacuum, leaves were either perfused with ultra-pure water (henceforward, “pure water”; 0.22um Thornton 200 CR; Millipore) or a 15 mM KCl solution. This concentration was chosen because the ion enhancement effect for stem xylem saturates at this concentration across species and is close to the maximum observed in measurements of natural xylem sap (Zwieniecki et al., 2001; Trifilo et al., 2008; Nardini et al., 2010). Both solutions were degassed overnight using a vacuum pump (Gast, Benton Harbor, MI, USA). Shoots of at least three leaves that had been rehydrated overnight were allowed to equilibrate in bags that had been humidified by exhaling into them to halt transpiration. The top and bottom leaves were excised and their water potentials were measured to indicate initial leaf water status. The middle leaf was measured for Kx; this leaf was placed in either pure water or the 15 mM KCl solution over a white-light transilluminator table and minor veins were severed between approximately 95% of tertiary veins throughout the leaf using a scalpel (Figure 1). These numbers of cuts far exceeded the amount shown by previous studies to short-circuit the outside-xylem pathways such that severing additional minor veins did not further increase the flow rate through the leaf during measurement (Sack et al., 2004; Nardini and Salleo, 2005; Nardini et al., 2005; Sack et al., 2005). Thus, only the conductance through the petiole and vein xylem is measured. This method has been used by multiple groups (Cochard et al., 2004; Gasco et al., 2004; Sack et al., 2004; Sack et al., 2005; Nardini et al., 2008; Scoffoni and Sack, 2015; Trifilo et al., 2016), and validated against the pressure probe method (Cochard et al., 2004).
Once cuts were made, the leaf was connected by tubing to the perfusing solution (either pure water or the 15 mM KCl solution) on a balance. The leaf was placed in a vacuum chamber, and five levels of partial vacuum (i.e., subatmospheric pressures) were applied (0.02, 0.03, 0.04, 0.05, and 0.06 MPa) and steady-state flows were obtained. Leaf temperature and area were recorded at the end of the measurement. We then calculated Kx as the slope of flow rates against vacuum pressures, and further normalized by leaf area and temperature (corrected to 25°C to adjust for the effect of temperature on the viscosity of water; Weast, 1974 ; Yang and Tyree, 1993; Sack et al., 2002).
Testing the ion effect on dehydrated leaves
We tested whether an ion enhancement of Kx could be observed at increasing tensions in Quercus agrifolia. For this species, we measured Kx under either pure water or 15 mM KCl as described above for 6 fully rehydrated leaves, 6 leaves dehydrated to approximately the turgor loss point, and 6 leaves dehydrated past the point of 80% percent loss of initial Kx. Further points were obtained using pure-water to construct the complete leaf xylem hydraulic vulnerability curve (which was previously published in Scoffoni and Sack, 2015). Our aim was not to test whether ion concentration in the xylem sap could impact air-seeding thresholds, as shoots were dehydrated containing their native sap. Rather, the aim of this experiment was to test for a potential methodological artefact in measurements of Kx vulnerability (i.e., response to dehydration) using pure water, as has been typically used in published studies.
Light microscopy sections of the leaf midrib
We obtained sections of leaf midribs for all seven species from previous studies of the same individuals and species (John et al., 2013; Scoffoni et al., 2017b). Briefly, sections of the middle of the midrib were embedded in resin, and transverse cross-sections 1 μm thick were obtained with a microtome, stained with Toluidine Blue O and imaged under light microscopy.
Statistics
To test for an ion-mediated effect on Kx and leaf water potential we performed a repeated-measures ANOVA across all seven species (R version 3.1.0). Two sample t-tests were performed to test for significance differences of the treatment within species. To test for ion-mediated effect on Kx vulnerability in Quercus agrifolia, we performed two sample t-tests for each of the three water potential intervals (Minitab 16).
Results
No significant ion-mediated enhancement of maximum leaf xylem hydraulic conductance (Kx) was found across the seven diverse species tested (Figure 2; repeated measures ANOVA p = 0.08). Because the overall effect was only marginally non-significant, we performed two sample t-tests comparing the treatment solutions for each species. Quercus agrifolia showed a 28% increase in Kx when perfused with 15 mmol KCl solution relative to pure water, increasing from 28.4 to 35.7 mmol m-2 s-1 MPa-1 (p = 0.008) whereas the other six species showed no effect (p-values ranged 0.08-0.96).
Figure 2. Testing for an ion-mediated enhancement of maximum leaf xylem hydraulic conductance across seven species diverse in phylogeny and drought tolerance. Samples measured under ultra-pure water are shown in black, while samples measured under 15 mM KCL solution are shown in white. Averages ± standard errors are shown for Kx. The p-value from repeated measures ANOVA is shown in the top right corner.
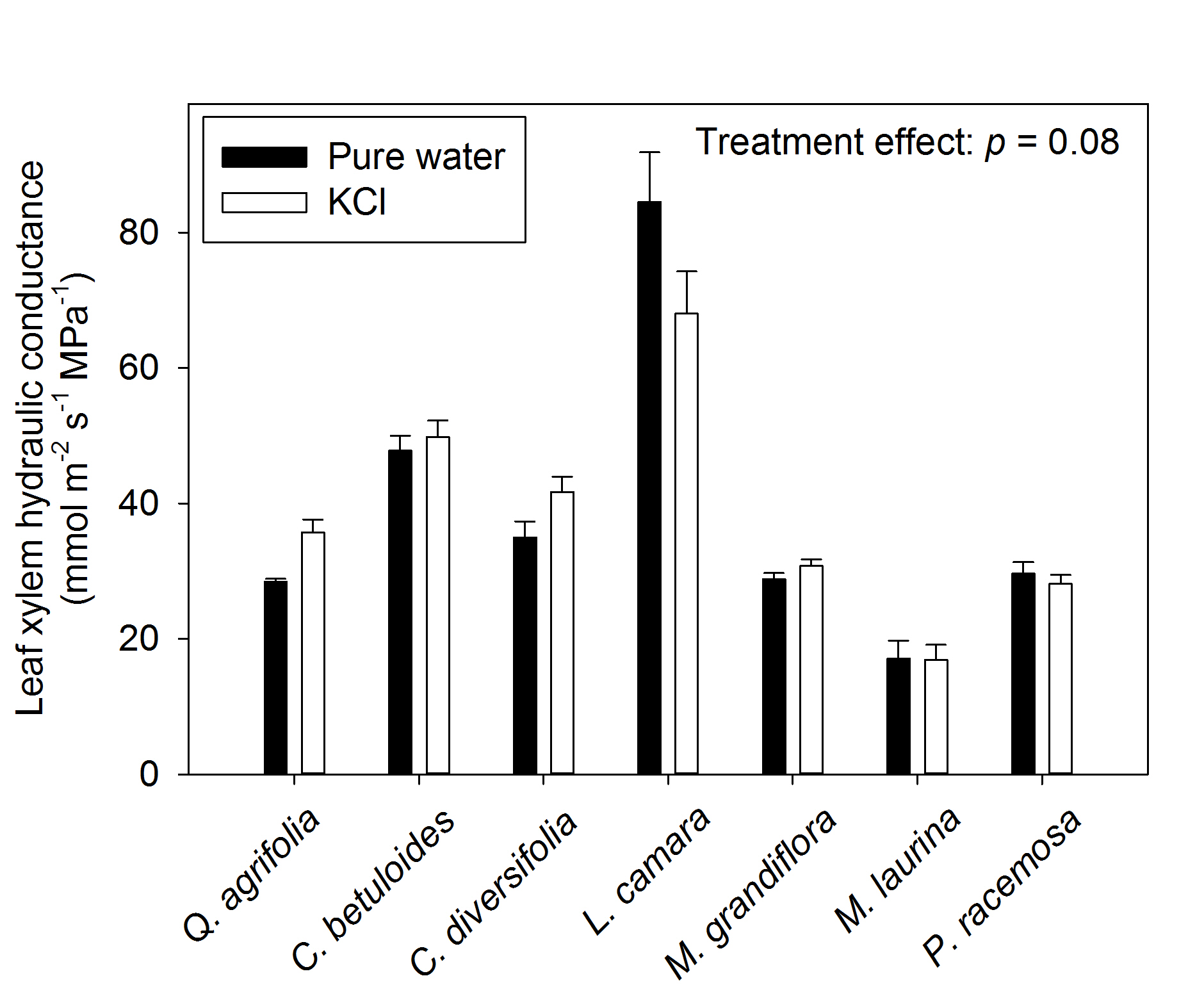
†Data from Scoffoni et al., 2014; Scoffoni et al., 2017a
We note that this enhancement was not caused as a result of differences in leaf water potential between treatments; water potentials differed between treatments across species overall (repeated measures ANOVA, p < 0.001) due to significant differences observed in Magnolia grandiflora. For that species, Kx measurements happened to be made under significantly more negative water potentials in pure water than the ion treatment (Table 1). The range of water potentials however did not cause Kx to decline; indeed, a vulnerability curve was constructed for the same individuals of M. grandiflora which showed that no decline in Kx occurred until -2MPa (Scoffoni et al., 2017a). Therefore, even though the range of leaf water potentials for Kx perfused under ultra-pure water was slightly more negative than that for the leaves perfused with high ion concentration solution, Kx would not have been affected by the slightly lower water potential. Further, no differences in water potential were found for 6/7 species (two sample t-tests: p= 0.59-0.84).
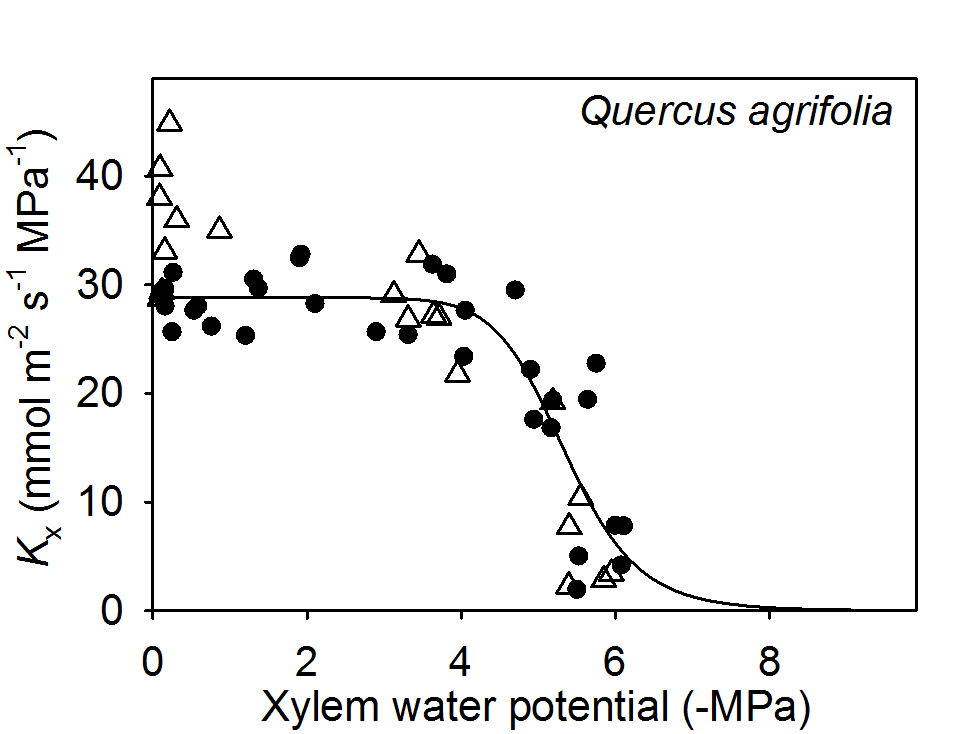
We tested whether perfusing dehydrated leaves with an ion solution instead of pure water had an impact on Kx (and thus potentially Kleaf) in Quercus agrifolia. We found no significant changes in Kx of leaves dehydrated to water potentials close to the turgor loss point of this species (-3.0 MPa; Scoffoni et al., 2012) nor to water potentials at which Kx has declined to around 80% (two sample t-test, p = 0.98 and 0.40 respectively; Figure 3).
Figure 3. Testing for an ion effect on the vulnerability of leaf xylem hydraulic conductance in Quercus agrifolia. White triangles are samples measured under 15 mM KCL while black circles are samples measured under ultra-pure water.
Discussion
Our results demonstrated that overall across seven species, there was no statistical effect of xylem sap ion concentration on Kx at full hydration (Repeated measures ANOVA). Further, no impact of ion concentration was found on Kx of dehydrated leaves of the one species tested. These contrast strongly with published results for stem xylem. On average across 35 angiosperm species, Kstem increased by 17.1 % with ion concentration (0-117 mM KCl across studies), ranging from 1.9% in Quercus ilex to 58% Tilia platyphyllos and with only 5/35 species showing an enhancement less than 5% (Nardini et al., 2011). Ion-mediated enhancement was first hypothesized to be driven by the swelling behavior of pectins in the inter-vessel pit membranes which would affect pit pore size, and thus resistance to water flow (Zwieniecki et al., 2001). However, that hypothesis has been regarded as unlikely given pectins do not occur in inter-vessel pit membranes (O'Brien, 1970; Esau and Evert, 2009; Kim and Daniel, 2013; Herbette et al., 2015). Indeed, all non-cellulosic elements (including pectins) are removed from the walls and pit membranes during wall hydrolysis in the late stages of xylem cell autolysis (O'Brien, 1970; Kim and Daniel, 2013). Pectins have been found to occur in annulus pit membranes, but only at the marginal region of the pits, where the surface is dense and is likely to contribute very little to the hydraulic conductance (Plavcova and Hacke, 2011; Herbette et al., 2015). It is thus unlikely that changes in pectin viscosity at these locations would explain the ion effect observed. A more recent hypothesis related the ion effect on Kstem to changes in electroviscosity in the pit pores (Jansen et al., 2011; Santiago et al., 2013). This theory is based on the fact that cations are always surrounding the pit pore membranes; when the flow solution has a higher ion concentration, fewer cations should be swept out of the pit pores, creating an opposing driving force to the pressure difference and reducing apparent hydraulic conductance.
In addition to ion effects mediated by pit pore resistance, anatomical correlates of the Kstem ion-mediated effect have been suggested. One study reported that across three evergreen species the enhancement was inversely related to vessel length, consistent with shorter vessels corresponding to sap flowing through a greater number of pit pores (Gasco et al., 2007). However, another study found that the ion enhancement of Kstem was unrelated to vessel length across 20 diverse angiosperm species (Jansen et al., 2011). In that study, a greater enhancement of Kstem was found for species with higher intervessel grouping, i.e., greater intervessel contact fraction and pit fraction (Jansen et al., 2011).
Such findings for the basis of the ion enhancement of Kstem suggest that the weak or absent ion enhancement of Kx at full leaf hydration may relate to the pit structure and vessel anatomy in the leaf vein xylem. We propose that the lack of ion effect on Kx could be explained by at least five hypotheses. First, pit apertures in leaf xylem conduits might be larger than those of stems, reducing the electroviscosity effect on hydraulic resistance. The only study to our knowledge that has described pore areas in leaf xylem conduits found pit aperture and pit membrane thickness to actually be larger in the stems than in the needles of Pinus pinaster (Bouche et al., 2016). However, a recent study on Pinus taeda showed that pit resistance accounted for a small portion of total vein resistance (30-45%; Domec et al., 2016), less than half the portion accounted for by pit resistance in stems on average for conifers (64%; Choat et al., 2008). Studies are needed to determine the differences in pit ultrastructure of the xylem across organs and vein orders for diverse species including angiosperms. A related second hypothesis is that water may flow through fewer pits in the leaf xylem as conduits can span from petiole through to the midrib, second- or third-order veins (Scoffoni and Sack, 2015; Scoffoni et al., 2016). Future studies need to look at the distribution of xylem conduit length across leaf vein orders and how this compares to that for stems. Third, a study found a high proportion of primary xylem vessels with extensible helical or annular secondary wall thickenings in the midrib of Acer saccharum (Choat et al., 2005). Such xylem anatomy with large areas of exposed primary cell membrane would likely reduce radial hydraulic resistance, which would lessen the effect of ion enhancement. Thus, studies are needed of the structure of xylem walls in the midribs and other vein orders for anatomically diverse species, to resolve how these compare to stems. Fourth, leaf midrib xylem is made up of a higher proportion of tracheids compared to vessels in midribs and conduits are arranged more closely (Figure 4) than in stems.
Figure 4. Light microscopy cross-sections of midribs for the seven study species. Xylem conduits are seen highly connected with one-another. These images point to the limitations of cross-sectional light microscopy for elucidating the ultrastructure of the xylem: different cross-sectional planes and/or microscopes are needed to determine pit ultrastructure and density, conduit lengths and wall ultrastructure any or all of which might influence ionic responses. Scale = 50μm.
Leaf minor veins tend to contain even fewer vessels or tracheids. With a lower proportion of vessels in leaves compared with stems, vessels would be more isolated which could reduce the ion enhancement (Jansen et al., 2011). Additionally, tracheids have greater membrane conductivity due to their pit structure (Hacke et al., 2004; Sperry et al., 2006). One study reported a tendency for tracheid bearing species to have lower ion enhancement of Kstem (Jansen et al., 2011). Future work is needed to quantify the relative abundance of tracheids vs. vessels across vein orders and how these compare to stems and vary across species. Fifth, the ion concentration in the leaf xylem sap may be higher than that in the stem if the xylem parenchyma or bundle sheath were to buffer the ion concentration (Secchi and Zwieniecki, 2012) such that even if pure water enters from the petiole, the ion concentration in the vein network may be enriched. Ion concentration might in fact vary across vein orders, as past studies have shown that minor veins (especially the free ending veins) could accumulate high ion concentration at the sites where water exits the apoplast and enters the symplast (up to 287 mM in a fifth order vein of Helianthus annuus; Canny, 1990, 1993). Future work is needed to determine the natural ion concentration across vein orders, and how higher ion concentrations might impact Kx.
Notably, one of our species (Quercus agrifolia) showed a 28 % increase in Kx at full hydration. This effect may be related to the nature of conduits (vessels vs. tracheids), conduit lengths (which would impact the degree to which water moves radially or longitudinally across conduits), pit ultrastructure and density and/or differences in natural ion concentration in the leaf veins. Detailed anatomical work on leaf vein xylem, and how it varies across vein orders is urgently needed to clarify potential differences in ion-mediated Kx enhancement across species. However, we note that such Kx enhancement observed under KCl perfusion in Q. agrifolia would be negligible at the whole leaf level, as the percent of leaf resistance within the xylem is only 14% in this species (Scoffoni et al., 2017a): a 28% increase of Kx would thus result in a Kleaf increase from 3.96 to 4.07 mmol m-2 s-1 MPa-1, i.e., an enhancement of <3%. Indeed, no ion enhancement of Kleaf was observed for two species tested (Sack et al., 2004) despite those species exhibiting a relatively high proportion of resistance inside their xylem (64 and 74% for Acer saccharum and Quercus rubra respectively; Sack et al., 2004).
The lack of ion effect on dehydrated leaves of Q. agrifolia suggests using pure water as perfusing solution would not lead to a measurement artifact, though future work should test this on more species. Even though Q. agrifolia showed a 28% enhancement of leaf Kx at full hydration, this effect became negligible at stronger tensions (Figure 3). This decoupling of the ion effect across water potentials suggests different mechanisms operating across leaf hydration states. Because the ion effect is higher given more isolated vessels (Jansen et al., 2011), if vessels were to embolize first, the ion-mediated effect could become negligible as vessels become non-functional such that sap would move mainly through highly interconnected tracheid elements. Micro-computed X-ray tomography of in-vivo embolism in the leaf petiole and midrib showed that larger conduits close to the pith often embolize first (Scoffoni et al., 2017b). Further information is needed on pore ultrastructure and the lengths and grouping of conduits in the different vein orders of leaves to clarify these effects. Moreover, studies are needed to test the impact of ion concentration on air-seeding thresholds in leaf veins. In stems, little impact of ion solution was found on stem hydraulic vulnerability to dehydration across seven species (Cochard et al., 2010), though no work has been done on leaf xylem.
The lack of an overall ion-enhancement of leaf xylem hydraulic conductance across the seven species tested implies that measurements of Kx and Kleaf are robust across solutions used, either pure water or ion solution. This result strongly supports whole plant hydraulic models that do not include hydraulic dependency on ion concentration (Sperry and Love, 2015; Christoffersen et al., 2016). Indeed, given that the enhancement effect is overall subtle in stems, and negligible in leaves, it would be expected to have little impact overall on whole plant hydraulic conductance. Future work is needed to test the effect in roots.
Acknowledgements
We thank Caetano Albuquerque, Craig Brodersen, Tom Buckley, Steven Jansen, Matthias Klepsch and Andrew McElrone for helpful insights during the preparation of the manuscript. We would like to thank two anonymous reviewers and Sylvain Delzon for their constructive comments. This work was supported by the US National Science Foundation (Awards #1146514 and #1457279).
References
- Bouche PS, Delzon S, Choat B, Badel E, Brodribb T, Burlett R, Cochard H, Charra-Vaskou K, Lavigne B, Shan L, Mayr S, Morris H, Torres-Ruiz JM, Zufferey V, Jansen S (2016) Are needles of Pinus pinaster more vulnerable to xylem embolism than branches? New insights from X-ray computed tomography. Plant, Cell & Environment 39: 860-870 doi:10.1111/pce.12680
- Canny MJ (1990) Fine veins of dicotyledon leaves as sites for enrichment of solutes of the xylem sap New Phytologist 115: 511-516 doi:10.1111/j.1469-8137.1990.tb00478.x
- Canny MJ (1993) The transpiration stream in the leaf apoplast: water and solutes. Philosophical Transactions of the Royal Society of London Series B-Biological Sciences 341: 87-100 doi:10.1098/rstb.1993.0094
- Choat B, Cobb AR, Jansen S (2008) Structure and function of bordered pits: new discoveries and impacts on whole-plant hydraulic function. New Phytologist 177: 608-625 doi:10.1111/j.1469-8137.2007.02317.x
- Choat B, Jansen S, Brodribb TJ, Cochard H, Delzon S, Bhaskar R, Bucci SJ, Feild TS, Gleason SM, Hacke UG, Jacobsen AL, Lens F, Maherali H, Martinez-Vilalta J, Mayr S, Mencuccini M, Mitchell PJ, Nardini A, Pittermann J, Pratt RB, Sperry JS, Westoby M, Wright IJ, Zanne AE (2012) Global convergence in the vulnerability of forests to drought. Nature 491: 752-755 doi:10.1038/nature11688
- Choat B, Lahr EC, Melcher P, Zwieniecki MA, Holbrook NM (2005) The spatial pattern of air seeding thresholds in mature sugar maple trees. Plant, Cell & Environment 28: 1082-1089 doi:10.1111/j.1365-3040.2005.01336.x
- Christoffersen BO, Gloor M, Fauset S, Fyllas NM, Galbraith DR, Baker TR, Kruijt B, Rowland L, Fisher RA, Binks OJ, Sevanto S, Xu CG, Jansen S, Choat B, Mencuccini M, McDowell NG, Meir P (2016) Linking hydraulic traits to tropical forest function in a size-structured and trait-driven model (TFS v.1-Hydro). Geoscientific Model Development 9: 4227-4255 doi:10.5194/gmd-9-4227-2016
- Cochard H, Badel E, Herbette S, Delzon S, Choat B, Jansen S (2013) Methods for measuring plant vulnerability to cavitation: a critical review. Journal of Experimental Botany 64: 4779-4791 doi:10.1093/jxb/ert193
- Cochard H, Herbette S, Hernandez E, Holtta T, Mencuccini M (2010) The effects of sap ionic composition on xylem vulnerability to cavitation. Journal of Experimental Botany 61: 275-285 doi:10.1093/jxb/erp298
- Cochard H, Nardini A, Coll L (2004) Hydraulic architecture of leaf blades: where is the main resistance? Plant Cell and Environment 27: 1257-1267 doi:10.1111/j.1365-3040.2004.01233.x
- Domec JC, Palmroth S, Oren R (2016) Effects of Pinus taeda leaf anatomy on vascular and extravascular leaf hydraulic conductance as influenced by N-fertilization and elevated CO2. Journal of Plant Hydraulics 3: e-007 doi:10.20870/jph.2016.e007
- Esau K, Evert RF (2009) Esau's plant anatomy: Meristems, cells and tissues of the plant body. Their structure, function and development. John Wiley & Sons
- Gasco A, Nardini A, Salleo S (2004) Resistance to water flow through leaves of Coffea arabica is dominated by extra-vascular tissues. Functional Plant Biology 31: 1161-1168
- Gasco A, Salleo S, Gortan E, Nardini A (2007) Seasonal changes in the ion-mediated increase of xylem hydraulic conductivity in stems of three evergreens: any functional role? Physiologia Plantarum 129: 597-606 doi:10.1071/FP04032
- Hacke UG, Sperry JS, Pittermann J (2004) Analysis of circular bordered pit function - II. Gymnosperm tracheids with torus-margo pit membranes. American Journal of Botany 91: 386-400 doi:10.3732/ajb.91.3.386
- Herbette S, Bouchet B, Brunel N, Bonnin E, Cochard H, Guillon F (2015) Immunolabelling of intervessel pits for polysaccharides and lignin helps in understanding their hydraulic properties in Populus tremula x alba. Annals of Botany 115: 187-199 doi:10.1093/aob/mcu232
- Jansen S, Gortan E, Lens F, Lo Gullo MA, Salleo S, Scholz A, Stein A, Trifilo P, Nardini A (2011) Do quantitative vessel and pit characters account for ion-mediated changes in the hydraulic conductance of angiosperm xylem? New Phytologist 189: 218-228 doi:10.1111/j.1469-8137.2010.03448.x
- John GP, Scoffoni C, Sack L (2013) Allometry of cells and tissues within leaves. American Journal of Botany: 100: 1936-1948 doi:10.3732/ajb.1200608
- Kim JS, Daniel G (2013) Developmental localization of homogalacturonan and xyloglucan epitopes in pit membranes varies between pit types in two poplar species. Iawa Journal 34: 245-262 doi:10.1163/22941932-00000021
- Nardini A, Grego F, Trifilo P, Salleo S (2010) Changes of xylem sap ionic content and stem hydraulics in response to irradiance in Laurus nobilis. Tree Physiology 30: 628-635 doi:10.1093/treephys/tpq017
- Nardini A, Ramani M, Gortan E, Salleo S (2008) Vein recovery from embolism occurs under negative pressure in leaves of sunflower (Helianthus annuus). Physiologia Plantarum 133: 755-764 doi:10.1093/treephys/tpq017 doi:10.1111/j.1399-3054.2008.01087.x
- Nardini A, Salleo S (2005) Water stress-induced modifications of leaf hydraulic architecture in sunflower: co-ordination with gas exchange. Journal of Experimental Botany 56: 3093-3101 doi:10.1093/jxb/eri306
- Nardini A, Salleo S, Andri S (2005) Circadian regulation of leaf hydraulic conductance in sunflower (Helianthus annuus L. cv Margot). Plant Cell and Environment 28: 750-759 doi:10.1111/j.1365-3040.2005.01320.x
- Nardini A, Salleo S, Jansen S (2011) More than just a vulnerable pipeline: xylem physiology in the light of ion-mediated regulation of plant water transport. Journal of Experimental Botany 62: 4701-4718 doi:10.1093/jxb/err208
- O'Brien TP (1970) Further observations on hydroloysis of the cell wall in the xylem. Protoplasma 69: 1-14 doi:10.1007/BF01276648
- Plavcova L, Hacke UG (2011) Heterogeneous distribution of pectin epitopes and calcium in different pit types of four angiosperm species. New Phytologist 192: 885-897 doi:10.1111/j.1469-8137.2011.03842.x
- Rockwell FE, Wheeler JK, Holbrook NM (2014) Cavitation and its discontents: opportunities for resolving current controversies. Plant physiology 164: 1649-1660 doi:10.1104/pp.113.233817
- Sack L, Ball MC, Brodersen C, Donovan L, Givnish TJ, Hacke U, Huxman TE, Jacobsen AL, Jansen S, Johnson DM, G. K, Lachenbruch B, Maurel C, McCulloch KA, McDowell N, McElrone AJ, Meinzer F, Melcher P, North GB, Pellegrini M, Pockman WT, Pratt RB, Rockwell FE, Sala A, Santiago LS, Scoffoni C, Sevanto SA, Sperry J, Spicer RA, Davies SJ, Tyerman SD, Way DA, Zweiniecki MA, Holbrook MN (2016) Plant water transport as a central hub from plant to ecosystem function: meeting report for “Emerging Frontiers in Plant Hydraulics” (Washington, DC, May 2015). Plant, Cell & Environment: In Press.
- Sack L, Holbrook NM (2006) Leaf hydraulics. Annual Review of Plant Biology 57: 361-381 doi:10.1146/annurev.arplant.56.032604.144141
- Sack L, Melcher PJ, Zwieniecki MA, Holbrook NM (2002) The hydraulic conductance of the angiosperm leaf lamina: a comparison of three measurement methods. Journal of Experimental Botany 53: 2177-2184 doi:10.1093/jxb/erf069
- Sack L, Streeter CM, Holbrook NM (2004) Hydraulic analysis of water flow through leaves of sugar maple and red oak. Plant Physiology 134: 1824-1833 doi:10.1104/pp.103.031203
- Sack L, Tyree MT (2005) Leaf hydraulics and its implications in plant structure and function. In Vascular Transport in Plants. eds N.M. Holbrook & M.A. Zweiniecki, Elsevier/Academic Press, Oxford, UK., pp 93–114 doi:10.1016/b978-012088457-5/50007-1
- Sack L, Tyree MT, Holbrook NM (2005) Leaf hydraulic architecture correlates with regeneration irradiance in tropical rainforest trees. New Phytologist 167: 403-413 doi:10.1111/j.1469-8137.2005.01432.x
- Santiago M, Pagay V, Stroock AD (2013) Impact of Electroviscosity on the Hydraulic Conductance of the Bordered Pit Membrane: A Theoretical Investigation. Plant Physiology 163: 999-1011 doi:10.1104/pp.113.219774
- Scoffoni C, Albuquerque C, Brodersen CR, Townes ST, John GP, Bartlett MK, Buckley TN, McElrone AJ, Sack L (2017a) Outside-xylem tissue vulnerability, not xylem embolism, controls leaf hydraulic decline with dehydration across diverse angiosperms. Plant Physiology 173 1197-1210 doi:10.1104/pp.16.01643
- Scoffoni C, Albuquerque C, Brodersen CR, Townes ST, John GP, Cochard H, Buckley TN, McElrone AJ, Sack L (2017b) Leaf vein xylem conduit diameter influences susceptibility to embolism and hydraulic decline. New Phytologist: doi:10.1111/nph.14256
- Scoffoni C, Chatelet DS, Pasquet-Kok J, Rawls M, Donoghue MJ, Edwards EJ, L. S (2016) Hydraulic basis for the evolution of photosynthetic productivity. Nature Plants 2, 16072
- Scoffoni C, McKown AD, Rawls M, Sack L (2012) Dynamics of leaf hydraulic conductance with water status: quantification and analysis of species differences under steady-state. Journal of Experimental Botany 63: 643-658 doi:10.1093/jxb/err270
- Scoffoni C, Sack L (2015) Are leaves “freewheelin'”? Testing for a Wheeler-type effect in leaf xylem hydraulic decline. Plant, Cell & Environment 38: 534-543 doi:10.1111/pce.12413
- Scoffoni C, Vuong C, Diep S, Cochard H, Sack L (2014) Leaf shrinkage with dehydration: coordination with hydraulic vulnerability and drought tolerance. Plant Physiology 164: 1772-1788 doi:10.1104/pp.113.221424
- Secchi F, Zwieniecki MA (2012) Analysis of xylem sap from functional (nonembolized) and nonfunctional (embolized) vessels of Populus nigra: chemistry of refilling. Plant Physiology 160: 955-964 doi:10.1104/pp.112.200824
- Sperry JS, Hacke UG, Pittermann J (2006) Size and function in conifer tracheids and angiosperm vessels. American Journal of Botany 93: 1490-1500 doi:10.3732/ajb.93.10.1490
- Sperry JS, Love DM (2015) What plant hydraulics can tell us about responses to climate-change droughts. New Phytologist 207: 14-27 doi:10.1111/nph.13354
- Trifilo P, Lo Gullo MA, Salleo S, Callea K, Nardini A (2008) Xylem embolism alleviated by ion-mediated increase in hydraulic conductivity of functional xylem: insights from field measurements. Tree Physiology 28: 1505-1512 doi:10.1093/treephys/28.10.1505
- Trifilo P, Raimondo F, Savi T, Lo Gullo MA, Nardini A (2016) The contribution of vascular and extra-vascular water pathways to drought-induced decline of leaf hydraulic conductance. Journal of Experimental Botany 67: 5029-5039 doi:10.1093/jxb/erw268
- Tyree MT, Zimmermann MH (2002) Xylem Structure and the Ascent of Sap. Springer, Berlin, Germany. doi:10.1007/978-3-662-04931-0
- van Ieperen W, van Meeteren U, van Gelder H (2000) Fluid ionic composition influences hydraulic conductance of xylem conduits. Journal of Experimental Botany 51: 769-776 doi:10.1093/jxb/51.345.769
- Weast RC (1974 ) Handbook of chemistry and physics. , 54th edn, Cleveland, OH: CRC Press.
- Wheeler JK, Huggett BA, Tofte AN, Rockwell FE, Holbrook NM (2013) Cutting xylem under tension or supersaturated with gas can generate PLC and the appearance of rapid recovery from embolism. Plant Cell and Environment 36: 1938-1949 doi:10.1111/pce.12139
- Yang SD, Tyree MT (1993) Hydraulic resistance in Acer saccharum shoots and its influence on leaf water potential and transpiration. Tree Physiology 12: 231-242 doi:10.1093/treephys/12.3.231
- Zimmermann MH (1978) Hydraulic architecture of some diffuse-porous trees. Canadian Journal of Botany-Revue Canadienne De Botanique 56: 2286-2295 doi:10.1139/b78-274
- Zwieniecki MA, Melcher PJ, Holbrook NM (2001) Hydrogel control of xylem hydraulic resistance in plants. Science 291: 1059-1062 doi:10.1126/science.1057175
Attachments
No supporting information for this articleArticle statistics
 Views: 2614
Views: 2614
Downloads
 PDF: 483
PDF: 483
 XML: 202
XML: 202
