Introduction

Stomatal response to environmental variation has a major influence on ecosystem carbon, water, and energy fluxes, and thus is important for global carbon and water cycles (Berry et al., 2010). Human-caused climate change is expected to intensify the hydrological cycle, which will greatly affect ecosystems in the 21^st century (Field et al., 2014). Plant stomatal conductance is a central physiological process that will mediate plant responses to changes in climate mean and extremes (Farquhar & Sharkey, 1982; Field et al., 1995; Franks et al., 2013; Keenan et al., 2013). Thus, stomatal behavior is likely to influence ecosystem response to climate change and also carbon cycle feedbacks of the terrestrial biosphere (Berry et al., 2010; Franks et al., 2013; Swann et al., 2016).

Stomatal response to drought – some combination of increasing atmospheric water demand through vapor pressure deficit (VPD) or decreasing soil water availability through falling soil water potential (ψ_s) – is a key component of plant drought responses (Tuzet et al., 2003; Sperry et al., 2016; Martin-StPaul et al., 2017). Stomatal closure is a critical way in which plants curtail water loss to avoid damage at shorter time-scales of seconds to days (Martin-StPaul et al., 2017). However, stomatal responses occur alongside a suite of longer time-scale responses, including canopy area adjustment (e.g. leaf shedding) (Wolfe et al., 2016), carbon allocation to increase root water uptake (Ledo et al., 2018), osmotic adjustment to tolerate lower water potentials (Bartlett et al., 2014), gene regulation and hormonal responses (Xu et al., 2010; Brodribb et al., 2014, 2016), and plastic changes in xylem anatomy over multiple years (Corcuera et al., 2004; Anderegg, 2015). Because stomatal conductance is influenced by a suite of whole-plant traits and signals, for example leaf water potential that is mediated by hydraulic transport from roots to leaves (e.g. Sperry et al., 2016), longer-term changes in plant drought responses have the potential to alter stomatal sensitivity to the environment. Thus, stomata have the opportunity to behave in a “Bayesian” manner by updating their behavior (e.g. water potentials at which stomatal closure begins) based on previous environmental conditions the plant has experienced, likely mediated by these longer-term plant responses such as biosynthesis of the hormone ABA

The vast majority of ecosystem models use empirical algorithms of stomatal conductance (Ball et al., 1987; Leuning, 1995; Sellers et al., 1996). Such models show reasonable predictive skill over the training conditions but may not be appropriate or skillful in prediction of stomatal conductance in changing and novel environmental conditions. In particular, many empirical models do not capture drought responses with high fidelity, likely due to a lack of representation of soil water potential and its impact on leaf water potential (Anderegg et al., 2017). Furthermore, it is not well-known how often or in what conditions the parameters of empirical models – for example, the slope of stomatal response to relative humidity or vapor pressure deficit – might vary, mediated by some of the well-documented processes described above, and thus would need to be “updated” in an ecosystem model to maintain predictive ability.

Optimal stomatal theories show promise for predicting stomatal conductance in future climates based on linking physiological processes with an evolutionary optimization to maximize plant fitness in varying environments (Medlyn et al., 2011; Prentice et al., 2014; Buckley et al., 2017; Anderegg et al., 2018; but see . A recent “carbon maximization” (CM) optimization has been proposed (Wolf et al., 2016) that posits that plants maximize carbon gain (A_N) minus the risk of hydraulic damage driven by low plant water potential (Θ(ψ)). This “risk of hydraulic damage” term may encompass a number of potential physiological mechanisms and is expected to increase sharply as water potentials decline. It is likely an integrated risk term, and thus is not tied to the probability or damage of a single event/outcome, but instead captures a suite of carbon costs that are likely to occur as hydraulic damage progresses. These may include the carbon costs of refilling embolized xylem (Broderson and McElrone, 2013), rebuilding new xylem to restore water transport after embolism (Brodribb and Cochard, 2009), direct damage of photosynthesis by low water potentials (Flexas et al., 2002), impaired phloem transport at low water potentials (Huang et al., 2018), and increased risk of drought-induced mortality at low water potentials (Anderegg et al., 2016; Martin-StPaul et al., 2017), among others.

This CM optimization (also called the “gain-risk” algorithm in Sperry et al. 2017) shows similar responses to environment as classic empirical models (Wolf et al., 2016; Sperry et al., 2017), reproduced hydraulic and gas exchange responses to a controlled drought experiment in Populus tremuloides with high accuracy (Venturas et al., 2018), and provided a major improvement in predictive ability (increase in R² of 0.11-0.25) over the classic marginal water use efficiency optimization when tested against a dataset of 34 woody plant species spanning global biomes (Anderegg et al., 2018). Because plant hydraulic algorithms are increasingly being incorporated into ecosystem and land surface models (Bonan et al., 2014; Xu et al., 2016; Fisher et al., 2018), this CM optimization has strong promise to link key components of plant drought physiology such as hydraulic traits and differences across species with gas exchange in a consistent framework that improves model prediction in novel climates (Anderegg et al., 2018).

Several key unresolved questions remain, however, concerning the CM optimization at longer time-scales and in varying environments. In particular, do these optimal stomatal parameters vary either 1) directly in response to drought drivers (i.e. VPD and/or ψ_s) and/or 2) in lagged response to drought drivers? This allows the examination of an interesting question: are stomata Bayesian in that they update their hydraulic risk “shadow price” (in the CM optimization, this shadow price is the marginal increase in carbon cost with a marginal drop in water potential – the partial derivative of the cost function; dΘ(ψ) in Eq. 6) as a function of previous climate? In addition, do these optimal stomatal parameters vary seasonally, such as between the wet and dry season in highly seasonal environments? The answers to these questions can both provide insight into the linkages between stomatal behavior and other longer-term plant drought responses and into the applicability of a single set of CM parameters in a large-scale ecosystem model over longer timescales.

Materials and Methods

Datasets

I used a subset of five species from a recently published dataset that compiled concurrent measurements of leaf-level gas exchange and plant water potentials (Anderegg et al., 2018). Two of the species were conifers (Pinus edulis and Juniperus monospermsa) from a semi-arid woodland in the southwestern United States (Limousin et al., 2013). Three of the species were angiosperms, including a temperate oak species (Quercus douglasii; ) from California, USA and two tropical species (Alphitonia excelsa and Brachychiton australis; (Choat et al., 2006)) from Australia (Table S1). These species were selected from the broader dataset because they had enough data to estimate stomatal model parameters at daily and/or seasonal time-scales. Briefly, these datasets contain concurrent measurements of stomatal conductance (g_s) and the key environmental variables needed to drive the plant model: photosynthetically active radiation (PAR), leaf-to-air vapor pressure deficit (VPD), carbon dioxide concentration at the leaf surface (Ca), predawn and midday leaf water potentials. In addition, the critical plant traits of the stem hydraulic vulnerability curve and the maximum carboxylation capacity (V_cmax) of leaves is known for these species and presented either in the original study (e.g. Limousin et al., 2013) or in the literature (Table S1 and see compilation in Anderegg et al., 2018).

Plant model with optimal stomatal behavior

To quantify the daily and seasonal shadow price (dΘ(ψ)), I used the plant model published in Anderegg et al. (2018) that couples hydraulic transport of water from the soil to the atmosphere with photosynthesis via the CM optimization. The model uses four equations that describe the dynamics of water transport and photosynthesis and a fifth equation from the CM optimization that allows solving for stomatal conductance at a given time-point with a given set of environmental conditions (for full details of the model, see Anderegg et al., 2018). Briefly, the model uses the C3 biochemical photosynthesis model described by Farquhar et al. , where assimilation (A) is the smallest of two limiting rates: w_c (CO₂/rubisco limitation) and w_j (light limitation):

${\mathrm{A}}_N\mathrm{ }=\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{n}(w_c,\mathrm{ }{w}_j)\mathrm{ }–\mathrm{ }{R}_d\mathrm{ }$
(1)

$w_c=\frac{V_{cmax} (C_i-{\mathrm{\Gamma }}^{*})}{C_i+K_c (1+\frac{O_i}{K_o})}$


$w_j= \frac{J ( C_i- {\mathrm{\Gamma }}^{*})}{4 ( C_i+2{\mathrm{\Gamma }}^{*})}$

where, C_i is the internal leaf CO₂ concentration, Γ^* is the CO₂ compensation point, K_c and K_o are Michaelis-Menten coefficients of the carboxylation and oxidation reactions performed by rubisco, O_i is the internal partial pressure of oxygen, J is the potential maximum rate of electron transport, calculated as in Medlyn et al. , and R_d is the rate of dark respiration calculated using a Q10 functional form. I used the standard implementation of the photosynthetic model presented in the freely available R package “plantecophys” .

For the second equation, the model uses a simplified version of Fick’s Law:

$A_N= g_s(C_a-C_i)/1.6$
        (2)

where g_s is stomatal conductance of the leaf to water vapor (mol m^-2 s^-1), 1.6 accounts for the difference in diffusion coefficients between water vapor and CO₂, and C_a is the partial pressure of CO₂ in the atmosphere. These equations assume that cuticular conductance is negligible and boundary layer and mesophyll conductances are much larger than stomatal conductance, which is likely reasonable for these species and environmental conditions (see Anderegg et al., 2018for additional assessment of these assumptions).

The third and fourth equations describe the water transport through the hydraulic continuum from soil to leaf and the water lost through stomatal conductance (transpiration):

$E= g_s(e_s-e_a)$
    (3)

where E is transpiration, e_a is the vapor pressure of water in the atmosphere at ambient temperature and relative humidity, and e_s is the vapor pressure of the saturated air space inside the leaf. Steady-state E is found by integrating the conductance function K() from soil water potential (here, measured plant pre-dawn water potential) to the leaf water potential (Sperry et al., 1998) :$E={\int }_{{\psi }_L}^{{\psi }_S}K\left(\psi \right)d\psi$    (4)

where ψ_s and ψ_L are the soil and leaf water potentials (MPa), respectively, and K() is the conductance function of the xylem, treated here as a Weibull with three parameters – scale and shape parameters that describe the hydraulic vulnerability curve – and Kmax, which was determined for each species by using the measured VPD, stomatal conductance, and predawn leaf water potential and finding the Kmax that best allowed prediction of midday leaf water potential using Equations (3) and (4).

The fifth and final equation in the model is the optimality equation that allows solving the system of equations to find a predicted stomatal conductance: $\frac{\partial A_N}{\partial g_s}= \frac{\partial \mathrm{\Theta }}{\partial g_s}$    (5)

where ($\partial$Θ/$\partial$g_s) was fit as the following function of leaf water potential:

$\frac{\partial \mathrm{\Theta }}{\partial g_s}= \frac{\partial \mathrm{\Theta }}{\partial {\psi }_L}\frac{\partial {\psi }_L}{\partial g_s}= \frac{\partial {\psi }_L}{\partial g_s} (a{\psi }_L+b)$
    (6)

where a and b are the key parameters to be fit. Critically, as shown in Wolf et al. (2016) and Anderegg et al. (2018), the a parameter is the slope of the marginal cost function and is thus the “shadow price” that I aim to estimate here.

Markov Chain Monte Carlo to find the shadow price

I used a Markov Chain Monte Carlo (MCMC) process to find the shadow price (parameter a in Eqn. 6) in the CM optimization for different species and time periods. This MCMC estimated the parameters a and b that provide the best fit between modelled stomatal conductance and measured stomatal conductance. First, for a given dataset, an initial guess of a and b was made. Initial guesses of a=0.1, and b=0 were selected as the initial guess as they are the closest to uninformative priors that still place a non-zero carbon price on drops in water potential. Next, for a given measurement (i.e. measurement of g_s and environmental drivers at a given time-point), an initial g_s of 0.010 mol m^-2 s^-1 was guessed. At that guess of g_s, the photosynthetic rate was then solved for using Equations 1-2 and the leaf water potential was solved for using Equations 3-4. The initial g_s was incremented slightly (+0.001 mol m^-2 s^-1) and the new A_N and ψ_L were found, allowing the calculation of the right hand side of Equation 5. Equation 6 is then solved with the current guesses of parameters a and b. Finally, a Newton-Raphson solver was implemented to find the stomatal conductance that solves Equation 5 – the predicted stomatal conductance by the model for that measurement. This process was repeated for all measurements within a given dataset and the sum of squared errors (SSE) was calculated between the predicted and observed g_s.

The MCMC was implemented to minimize the SSE between predicted and observed g_s. After preliminary testing to find the ideal step size (typically 0.1-1 depending on species) in guesses of parameters a and b that led to a ~50% acceptance probability, I initiated three chains of 5,000 steps for every dataset and compared chains to ensure rapid mixing by testing that the ratio of inter-chain to intra-chain variances was close to 1. I then discarded the first 1,000 steps to avoid initial conditions and thinned the chains by a factor of ~10 to remove effects of autocorrelation before calculating the mean and confidence intervals for parameter a for each dataset.

Analyses

To examine diurnal changes in the shadow price, I performed the MCMC on each day for the three species with adequate daily data (>8 measurements within a day). I extracted the maximum likelihood (lowest SSE) parameter a from the MCMC output and I performed ordinary least squares regression of the shadow price against mean VPD and mean predawn leaf water potential, which can be assumed to be approximately Ψ_s if plant water potential has equilibrated with the soil (e.g. minimal nighttime transpiration) (Donovan et al., 2001).

For Pinus edulis and Juniperus monosperma, which had enough daily data to perform model selection and multi-variate models and almost identical measurement dates and frequencies (Table S2), I further calculated a number of climate and plant stress metrics for that day (which includes measurements from several trees): 1) minimum midday leaf water potential recorded for any tree, 2) maximum midday leaf water potential recorded for any tree, 3) minimum leaf predawn water potential recorded for any tree, 4) mean leaf predawn water potential of all trees, 5) maximum leaf predawn water potential recorded for any tree, 6) minimum VPD, 7) mean VPD, 8) maximum VPD, 9) number of measurements made that day, and 10) date. As a subsequent analysis to assess the role of lagged drought stress and stomatal response, I added the minimum and maximum VPD and leaf predawn and midday water potentials of the previous measurement date to the above current-measurement variables for model selection. Measurements on these species typically came in 2-3 day periods spaced about a month apart over the growing season (Table S2).

To determine which variables best predicted daily shadow price variation, I performed a model selection procedure with two sets of variables: 1) current-day variables only and 2) current and lagged variables together. Because model selection can be adversely affected by strongly collinear predictor variables, I first removed collinear predictor variables using a standard procedure (Anderegg et al., 2013; Dahlin et al., 2013). I constructed a correlation matrix of the pairwise correlations between all predictor variables. Whenever any two variables were strongly correlated (r>0.7), the correlation between each of those variables and the dependent variable (shadow price parameter a) was calculated. The variable with a lower correlation with the dependent variable was dropped. Once a set of non-collinear variables was generated, I then performed stepwise model selection, both forward and backward, using the Akaike Information Criterion. This yields the most parsimonious model that minimizes the information loss and also penalizes models for each additional predictor. All analyses were performed in the R statistical environment. Model selection was performed using the stepAIC function in the MASS library (Ripley et al., 2013).

To assess if the shadow price varied between wet and dry periods (a seasonal analysis), I performed the MCMC to estimate parameter a for each species on the driest and wettest half of the data, stratified by predawn leaf water potential. For the tropical species and temperate oak species, this roughly corresponded to “wet” and “dry” seasons (Choat et al., 2006). For the temperate conifers, this stratified the data by relatively wet and benign winter or late-summer monsoon periods versus hot and dry spring and early summer periods (Limousin et al., 2013).

Results

Daily estimates of the slope of the cost function (a) did not vary predictably as a function of VPD or ψ_s (p>0.05 for all regressions; Fig. 1, Fig. 2) in the three species with adequate data to estimate daily parameters. There was substantial variation in the slope across days and larger variation in the range of slopes across species, but this variation was unrelated to increasing water stress. The marginal cost increased slightly but insignificantly at higher VPDs in all species and increased slightly but insignificantly as soil water potential declined in two of three species (Fig. 1, Fig. 2).

Figure 1: Stomatal cost function slope compared to vapor pressure deficit.

Save View full size Expand inline Collapse inline

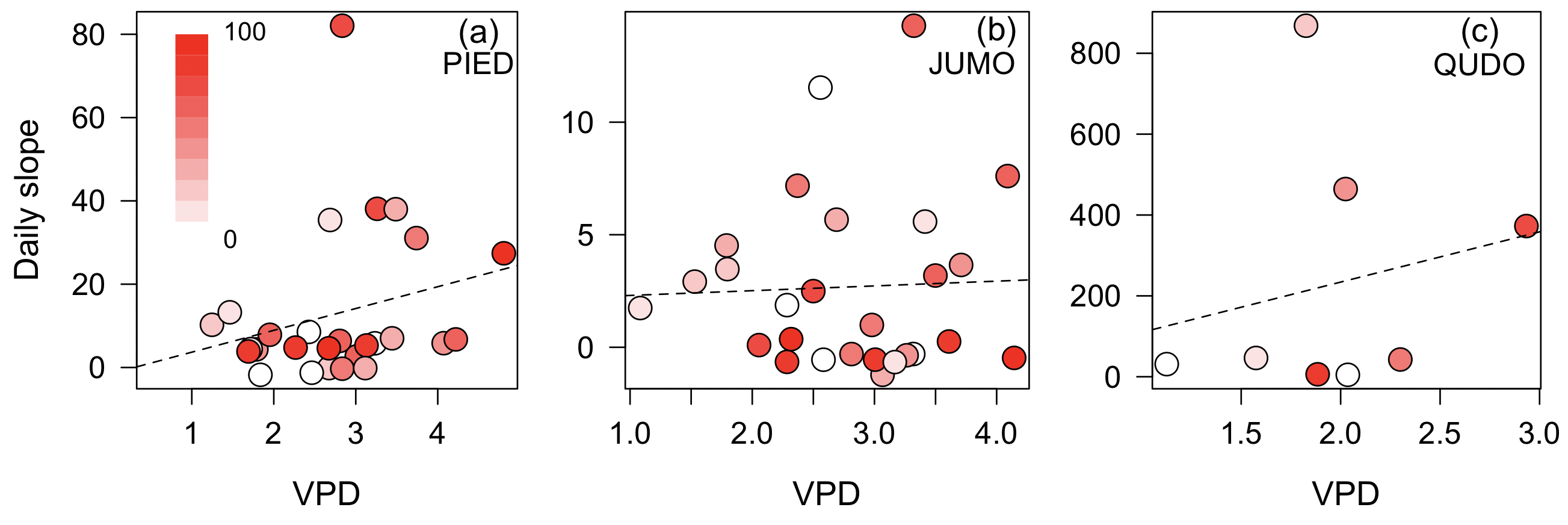
The slope of the stomatal cost function is uncorrelated with vapor pressure deficit (VPD; kPa) across the tree species Pinus edulis (a), Juniperus monosperma (b), and Quercus douglasii (c). Each point is a day and the color of points is the predawn leaf (e.g. soil) water potential percentile (color bar) for that day and redder colors indicate more negative water potentials. Lines are the OLS best fit and are not statistically significant.

Figure 2: Stomatal cost function slope compared to predawn water potential.

Save View full size Expand inline Collapse inline

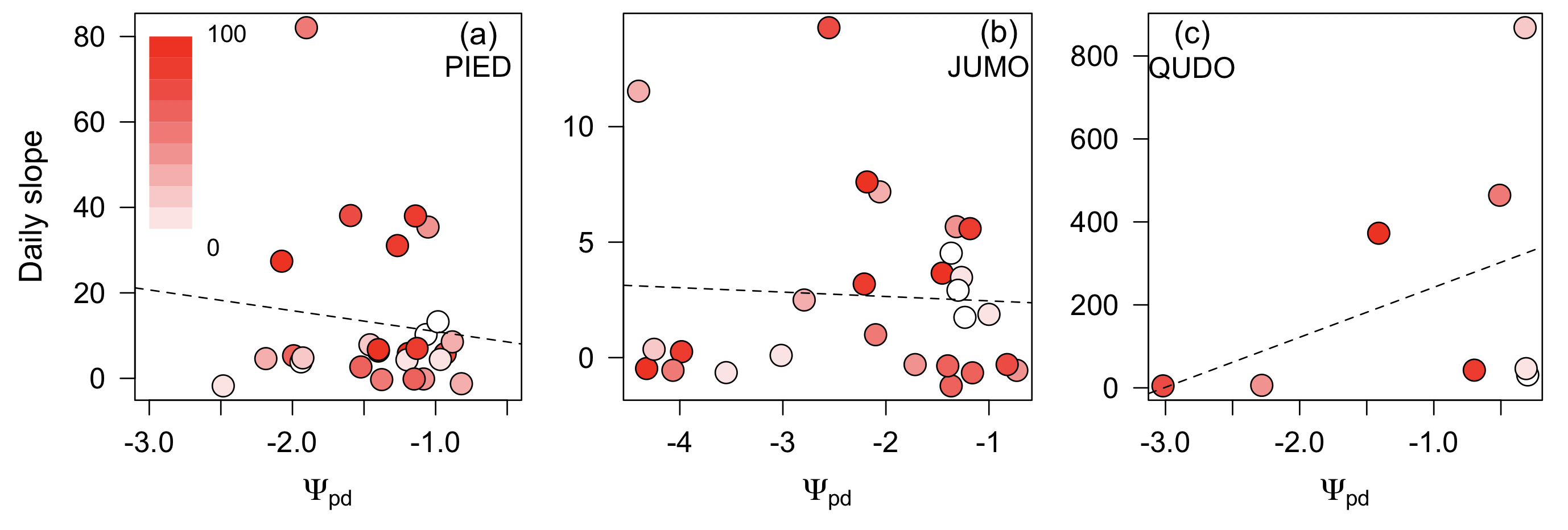
The slope of the stomatal cost function is uncorrelated with predawn leaf water potential (Ψ_pd; MPa ) across the tree species Pinus edulis (a), Juniperus monosperma (b), and Quercus douglasii (c). Each point is a day and the color of points is the vapor pressure deficit (color bar) for that day and redder colors indicate higher VPD values. Lines are the OLS best fit and are not statistically significant.

While the predictive ability of the slope of the cost function was fairly low overall in both species with a multitude of daily data (P. edulis and J. monosperma), lagged drought indicators improved predicting cost functions (Table 1). For P. edulis, the best fitting and most parsimonious model selected by AIC with non-lagged variables explained 17% of the variation (p=0.04) and contained the highest leaf water potential recorded during that day, the number of stomatal conductance measurements, and the date. Considering lagged variables, model selection yielded the same three current-day predictor variables and also the previous date’s lowest measured leaf water potential, and the variance explained rose to 25% (p=0.03, ΔAIC>2) (Table 1). For J. monosperma, the best current-day model explained only 12% of the variation and was marginally significant (p=0.1). This model included the variables highest leaf water potential recorded during that day and the date (Table 1). Considering lagged variables as well, the most parsimonious model included the two above variables and also the maximum VPD of the previous measurement date. The variance explained in this model rose to 23% (p=0.01; ΔAIC>2) (Table 1).

Examining seasonal variation in cost functions, I observed moderate seasonal differences in cost functions in the two gymnosperm species (p<0.01), but not in the three angiosperm species (Fig. 3). Uncertainty in cost functions was somewhat larger in the wetter periods than drier periods, especially in the tropical angiosperm species (Fig. 3). A sensitivity analysis with an alternate vulnerability curve for Q. douglasii (Skelton et al., 2017) showed predicted gs values that were very similar to the ones presented here (R²=0.99). One potential reason for the detection of seasonal differences in the gymnosperm species may be due to biome-level differences in climate, whereby the gymnosperm species experienced a much larger variation of water potential and much greater declines in water potential during the drier periods (Fig. 4).

Despite slight seasonal differences in the gymnosperm species, the predictive ability of a single set of CM parameters at a species level was quite similar to the model allowing for seasonal differences in CM parameters (R²_species=0.48; R²_seas=0.50; Fig. 5). Indeed, the predictive differences between the models was minimal; the root mean squared error difference to the models was 0.002 mol m^-2 sec^-1 (RMSE_species=0.077; RMSE_seas=0.075). Predictive ability was strongest in the two gymnosperm and the temperate oak species and substantially lower in the two tropical species.

Figure 3: Seasonal estimates of the stomatal cost function slope parameter.

Save View full size Expand inline Collapse inline

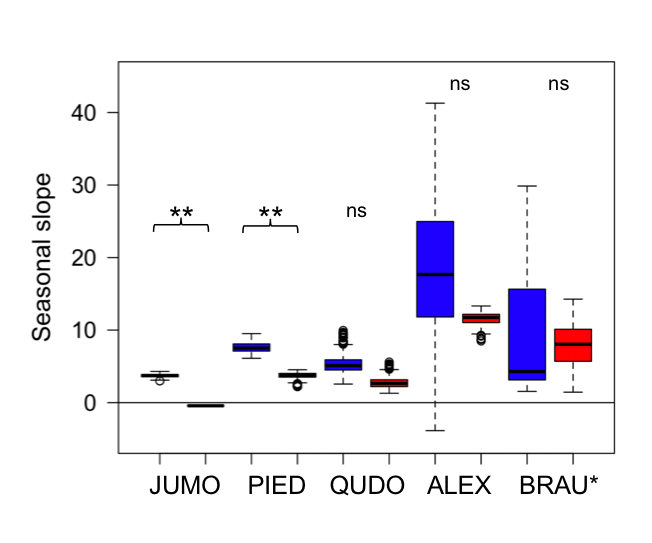
Seasonal estimates of the stomatal cost function slope parameter in the wet (blue) and dry (red) periods for Juniperus monosperma (JUMO; N=576), Pinus edulis (PIED; N=511), Quercus douglasii (QUDO; N=166), Alphitonia excelsa (ALEX; N=173) and Brachychiton australis (BRAU; N=100). Black line is the median; boxes the interquartile range, and error bars show the highest and lowest value of the data excluding outliers. Stars indicate statistical significance (i.e. 95% confidence intervals do not overlap)

Figure 4: Range in predawn leaf water potential for all species.

Save View full size Expand inline Collapse inline

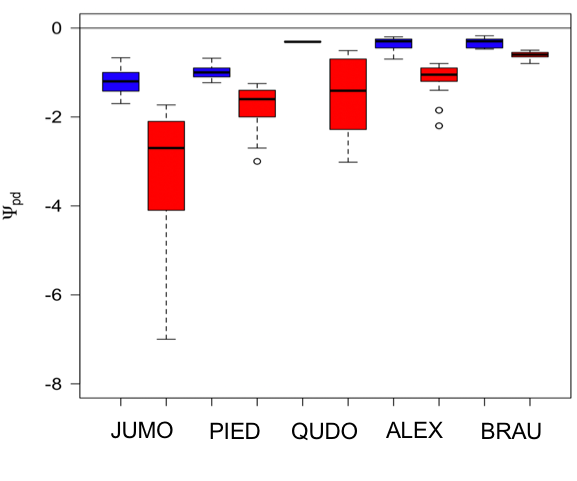
Range in predawn leaf water potential for all species in the wet (blue) and dry (red) periods for Juniperus monosperma (JUMO; N=576), Pinus edulis (PIED; N=511), Quercus douglasii (QUDO; N=166), Alphitonia excelsa (ALEX; N=173) and Brachychiton australis (BRAU; N=100). Black line is the median; boxes the interquartile range, and error bars show the highest and lowest value of the data excluding outliers.

Figure 5: Observed versus predicted stomatal conductance from the CM optimization.

Save View full size Expand inline Collapse inline

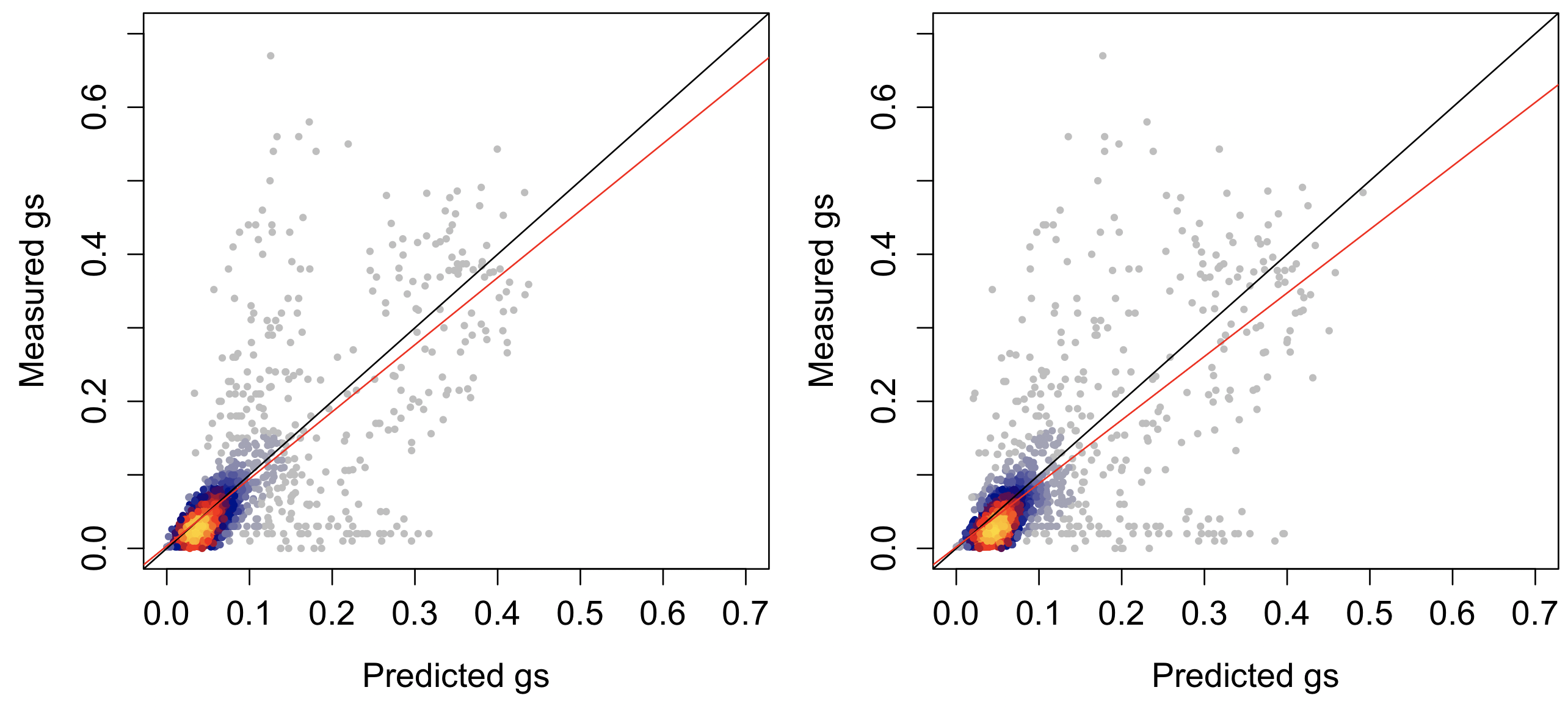
Observed versus predicted stomatal conductance (gs; mol m^-2 sec^-1) for all five species where a separate set of parameters are used for wet and dry periods for each species (left) or a single set of parameters is used for each species (right). Colors show the density of points with gray and blue as low density and red to yellow as highest density. Red line is the ordinary least squares regression best fit and black line is the 1:1 line.

Discussion

Predicting stomatal conductance across multiple time-scales is a central aim of many vegetation models and may be informed by optimal stomatal models. I analyzed the parameters of an optimal stomatal model at multiple time-scales and reached three central conclusions. First, the key parameter of the CM optimal stomatal model – the marginal cost of water potential – does not change predictably in response to VPD and ψ_s in the species analyzed here. Second, there is some evidence for the influence of lagged variables on stomatal model parameters, indicating stomata might be behaving in a somewhat Bayesian manner, though the evidence is not strong. Finally, while slight seasonal changes in parameters were detected in two of five species, a single set of species-level parameters worked nearly as well for prediction of stomatal conductance across all time-scales.

The longest and most detailed datasets of the two conifer species revealed that including previous date’s lowest leaf water potential (P. edulis) or the previous date’s maximum VPD (J. monosperma) improved prediction of the current date’s cost function slope. Previous research has documented changes in gas exchange and stomatal conductance following severe droughts, even if leaf water potential recovers (Resco et al., 2009) and, indeed, lingering effects of canopy area, hydraulic conductance, or hormonal adjustment (e.g. ABA) would likely influence stomatal conductance responses to environment (Brodribb et al., 2016; Skelton et al., 2017). Given that substantial canopy area adjustment was not observed during the measurement record and that measurements were typically ~1 month apart (Table S2) (Limousin et al., 2013), the lingering effects of previous measurements are more likely changes in tissue allocation or damage (e.g. embolism) or potentially signaling related. It is notable, however, that there was large diurnal variation in these cost function parameters at daily timescales, which is likely due to small number of data points per day.

In the CM optimization, the cost that stomata aim to avoid is formulated as an instantaneous carbon cost, but most likely includes multiple aspects of hydraulic “risk” that could play out over longer time periods (Wolf et al., 2016; Sperry et al., 2017; Anderegg et al., 2018). Sperry et al., (2017) use species’ hydraulic vulnerability curves as the risk/cost function, which drives stomata to close in order to avoid loss of hydraulic conductivity due to embolism. Much more research is needed to understand the physiology underpinning specific hydraulic risks. There are multiple potential physiological mechanisms underpinning how the hydraulic risk/cost function could increase as water potentials fall. These include direct impairment of photosynthesis , phloem loading limitations due to decreased carbon sink activity (Nikinmaa et al., 2013), leaf or xylem structural damage (including embolism), energetic costs of maintaining osmotic regulation (Hinckley et al., 1980; Bartlett et al., 2014), and shadow prices of future losses in photosynthesis due to hydraulic damage and risk of mortality (Anderegg et al., 2018).

The CM optimization shows substantial promise for inclusion into next-generation ecosystem models because plant hydraulic transport provides a mechanistic way to simulate drought stress on plants from easily measurable traits and because the CM optimization showed the highest predictive ability of stomatal conductance in previous analyses (Anderegg et al. 2018). The findings here that seasonal differences in parameters are minimal and do not greatly affect accuracy of prediction of leaf-level stomatal conductance lend further support. Intra-specific variation and plasticity in plant drought responses and hydraulic transport are likely to be important in many contexts and may not be captured in the relatively short (1-2 year) datasets included here. Plasticity or variation can be incorporated hydraulic-enabled ecosystem models through hydraulic trait variation, which will allow the CM optimization to flexibly predict stomatal conductance in a wide array of environments.

Acknowledgements

I thank Y.S. Lin and B. Medlyn for compiling the original database from which several species’ stomatal conductance data were obtained for this study and J. Limousin, B. Choat, and D. Baldocchi for sharing data. I further thank S. MacAdam and N. Martin for their insightful reviews. W.R.L.A. acknowledges funding from the University of Utah Global Change and Sustainability Center, NSF Grant 1714972, and the USDA National Institute of Food and Agriculture, Agricultural and Food Research Initiative Competitive Programme, Ecosystem Services and Agro-ecosystem Management, grant no. 2018-67019-27850.

References

• Anderegg WR. 2015. Spatial and temporal variation in plant hydraulic traits and their relevance for climate change impacts on vegetation. New Phytologist 205: 1008–1014.
• Anderegg LDL, Anderegg WRL, Abatzoglou J, Hausladen AM, Berry JA. 2013. Drought characteristics’ role in widespread aspen forest mortality across Colorado, USA. Global Change Biology 19: 1526–1537.
• Anderegg, WRL, et al. 2016. Meta-analysis reveals that hydraulic traits explain cross-species patterns of drought-induced tree mortality across the globe. Proceedings of the National Academy of Sciences. 113: 5024-5029.
• Anderegg WRL, Wolf A, Arango-Velez A, Choat B, Chmura DJ, Jansen S, Kolb T, Li S, Meinzer F, Pita P. 2017. Plant water potential improves prediction of empirical stomatal models. PloS one 12: e0185481.
• Anderegg WR, Wolf A, Arango-Velez A, Choat B, Chmura DJ, Jansen S, Kolb T, Li S, Meinzer FC, Pita P. 2018. Woody plants optimise stomatal behaviour relative to hydraulic risk. Ecology letters 21: 968–977
• Ball JT, Woodrow IE, Berry JA. 1987. A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. In: Progress in photosynthesis research. Springer, 221–224.
• Bartlett MK, Zhang Y, Kreidler N, Sun S, Ardy R, Cao K, Sack L. 2014. Global analysis of plasticity in turgor loss point, a key drought tolerance trait. Ecology letters 17: 1580–1590.
• Berry JA, Beerling DJ, Franks PJ. 2010. Stomata: key players in the earth system, past and present. Current opinion in plant biology 13: 232–239.
• Bonan GB, Williams M, Fisher RA, Oleson KW. 2014. Modeling stomatal conductance in the earth system: linking leaf water-use efficiency and water transport along the soil–plant–atmosphere continuum. Geoscientific Model Development 7: 2193–2222.
• Brodersen C, and A McElrone. 2013. Maintenance of xylem network transport capacity: a review of embolism repair in vascular plants. Frontiers in Plant Science. 4: 108.
• Brodribb, TJ, and H Cochard. 2009. Hydraulic failure defines the recovery and point of death in water-stressed conifers. Plant Physiology 149: 575–584.
• Brodribb TJ, McAdam SA. 2017. Evolution of the stomatal regulation of plant water content. Plant physiology 174: 639–649.
• Brodribb TJ, McAdam SA, Carins Murphy MR. 2016. Xylem and Stomata, Coordinated Through Time and Space. Plant, Cell & Environment 40: 872–880
• Brodribb TJ, McAdam SA, Jordan GJ, Martins SC. 2014. Conifer species adapt to low-rainfall climates by following one of two divergent pathways. Proceedings of the National Academy of Sciences 111: 14489–14493.
• Buckley TN, Sack L, Farquhar GD. 2017. Optimal plant water economy. Plant, cell & environment 40: 881–896.
• Choat B, Ball MC, Luly JG, Donnelly CF, Holtum JA. 2006. Seasonal patterns of leaf gas exchange and water relations in dry rain forest trees of contrasting leaf phenology. Tree Physiology 26: 657–664.
• Corcuera L, Camarero J, Gil-Pelegrín E. 2004. Effects of a severe drought on Quercus ilex radial growth and xylem anatomy. Trees 18: 83–92.
• Cowan IR, Farquhar GD. 1977. Stomatal function in relation to leaf metabolism and environment. In: Symposia of the Society for Experimental Biology. 471.
• Dahlin KM, Asner GP, Field CB. 2013. Environmental and community controls on plant canopy chemistry in a Mediterranean-type ecosystem. Proceedings of the National Academy of Sciences 110: 6895–6900.
• Donovan L, Linton M, Richards J. 2001. Predawn plant water potential does not necessarily equilibrate with soil water potential under well-watered conditions. Oecologia 129: 328–335.
• Duursma RA. 2015. Plantecophys-An R Package for Analysing and Modelling Leaf Gas Exchange Data. PloS one 10: e0143346.
• Farquhar GD, Caemmerer S, Berry JA. 1980. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149: 78–90.
• Farquhar GD, Sharkey TD. 1982. Stomatal conductance and photosynthesis. Annual review of plant physiology 33: 317–345.
• Field CB, Barros VR, Dokken DJ, Mach KJ, Mastrandrea MD, Bilir TE, Chatterjee M, Ebi KL, Estrada YO, Genova RC, et al. 2014. IPCC, 2014: Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
• Field CB, Jackson RB, Mooney HA. 1995. Stomatal responses to increased CO2: implications from the plant to the global scale. Plant, Cell & Environment 18: 1214–1225.
• Fisher RA, Koven CD, Anderegg WR, Christoffersen BO, Dietze MC, Farrior CE, Holm JA, Hurtt GC, Knox RG, Lawrence PJ. 2018. Vegetation demographics in Earth System Models: A review of progress and priorities. Global change biology 24: 35–54.
• Flexas J, Medrano H. 2002. Drought-inhibition of photosynthesis in C3 plants: stomatal and non-stomatal limitations revisited. Annals of botany 89: 183–189.
• Franks PJ, Adams MA, Amthor JS, Barbour MM, Berry JA, Ellsworth DS, Farquhar GD, Ghannoum O, Lloyd J, McDowell N. 2013. Sensitivity of plants to changing atmospheric CO2 concentration: from the geological past to the next century. New Phytologist 197: 1077–1094.
• Franks, PJ, et al. 2018. Comparing optimal and empirical stomatal conductance models for application in Earth system models. Global Change Biology. doi: 10.1111/gcb.14445
• Hinckley TM, Duhme F, Hinckley AR, Richter H. 1980. Water relations of drought hardy shrubs: osmotic potential and stomatal reactivity. Plant, Cell & Environment 3: 131–140.
• Keenan TF, Hollinger DY, Bohrer G, Dragoni D, Munger JW, Schmid HP, Richardson AD. 2013. Increase in forest water-use efficiency as atmospheric carbon dioxide concentrations rise. Nature 499: 324–327.
• Ledo A, Paul KI, Burslem DF, Ewel JJ, Barton C, Battaglia M, Brooksbank K, Carter J, Eid TH, England JR. 2018. Tree size and climatic water deficit control root to shoot ratio in individual trees globally. New Phytologist 217: 8–11.
• Leuning R. 1995. A critical appraisal of a combined stomatal-photosynthesis model for C3 plants. Plant, Cell & Environment 18: 339–355.
• Limousin J, Bickford CP, Dickman LT, Pangle RE, Hudson PJ, Boutz AL, Gehres N, Osuna JL, Pockman WT, McDowell NG. 2013. Regulation and acclimation of leaf gas exchange in a piñon–juniper woodland exposed to three different precipitation regimes. Plant, Cell & Environment 36: 1812–1825.
• Martin‐StPaul N, S Delzon, H Cochard. 2017. Plant resistance to drought depends on timely stomatal closure. Ecology Letters 20: 1437-1447.
• Medlyn BE, Dreyer E, Ellsworth D, Forstreuter M, Harley PC, Kirschbaum MUF, Le Roux X, Montpied P, Strassemeyer J, Walcroft A, et al. 2002. Temperature response of parameters of a biochemically based model of photosynthesis. II. A review of experimental data. Plant, Cell & Environment 25: 1167–1179.
• Medlyn BE, Duursma RA, Eamus D, Ellsworth DS, Prentice IC, Barton CVM, Crous KY, De Angelis P, Freeman M, Wingate L. 2011. Reconciling the optimal and empirical approaches to modelling stomatal conductance. Global Change Biology 17: 2134–2144.
• Nikinmaa E, HÖLttÄ T, Hari P, Kolari P, MÄKelÄ A, Sevanto S, Vesala T. 2013. Assimilate transport in phloem sets conditions for leaf gas exchange. Plant, Cell & Environment 36: 655–669.
• Prentice IC, Dong N, Gleason SM, Maire V, Wright IJ. 2014. Balancing the costs of carbon gain and water transport: testing a new theoretical framework for plant functional ecology. Ecology Letters 17: 82–91.
• Resco V, Ewers BE, Sun W, Huxman TE, Weltzin JF, Williams DG. 2009. Drought-induced hydraulic limitations constrain leaf gas exchange recovery after precipitation pulses in the C3 woody legume, Prosopis velutina. New Phytologist 181: 672–682.
• Ripley B, Venables B, Bates DM, Hornik K, Gebhardt A, Firth D, Ripley MB. 2013. Package ‘MASS’. CRAN Repos. Httpcran R-Proj. OrgwebpackagesMASSMASS Pdf.
• Sellers PJ, Randall DA, Collatz GJ, Berry JA, Field CB, Dazlich DA, Zhang C, Collelo GD, Bounoua L. 1996. A Revised Land Surface Parameterization (SiB2) for Atmospheric GCMS. Part I: Model Formulation. Journal of Climate 9: 676–705.
• Skelton RP, Brodribb TJ, McAdam SA, Mitchell PJ. 2017. Gas exchange recovery following natural drought is rapid unless limited by loss of leaf hydraulic conductance: evidence from an evergreen woodland. New Phytologist 215: 1399–1412.
• Sperry JS, Adler FR, Campbell GS, Comstock JP. 1998. Limitation of plant water use by rhizosphere and xylem conductance: results from a model. Plant, Cell & Environment 21: 347–359.
• Sperry JS, Venturas MD, Anderegg WR, Mencuccini M, Mackay DS, Wang Y, Love DM. 2017. Predicting stomatal responses to the environment from the optimization of photosynthetic gain and hydraulic cost. Plant, cell & environment 40: 816–830.
• Sperry JS, Wang Y, Wolfe BT, Mackay DS, Anderegg WR, McDowell NG, Pockman WT. 2016. Pragmatic hydraulic theory predicts stomatal responses to climatic water deficits. New Phytologist 212: 577–589.
• Swann AL, Hoffman FM, Koven CD, Randerson JT. 2016. Plant responses to increasing CO2 reduce estimates of climate impacts on drought severity. Proceedings of the National Academy of Sciences 113: 10019–10024.
• Tuzet A, Perrier A, Leuning R. 2003. A coupled model of stomatal conductance, photosynthesis and transpiration. Plant, Cell & Environment 26: 1097–1116.
• Venturas, MD, et al. 2018. A stomatal control model based on optimization of carbon gain versus hydraulic risk predicts aspen sapling responses to drought. New Phytologist. doi: doi.org/10.1111/nph.15333
• Wolf A, Anderegg WRL, Pacala SW. 2016. Optimal stomatal behavior with competition for water and risk of hydraulic impairment. Proceedings of the National Academy of Sciences 113: E7222–E7230.
• Wolfe BT, Sperry JS, Kursar TA. 2016. Does leaf shedding protect stems from cavitation during seasonal droughts? A test of the hydraulic fuse hypothesis. New Phytologist 212: 1007–1018.
• Xu L, Baldocchi DD. 2003. Seasonal trends in photosynthetic parameters and stomatal conductance of blue oak (Quercus douglasii) under prolonged summer drought and high temperature. Tree physiology 23: 865–877.
• Xu X, Medvigy D, Powers JS, Becknell JM, Guan K. 2016. Diversity in plant hydraulic traits explains seasonal and inter-annual variations of vegetation dynamics in seasonally dry tropical forests. New Phytologist 212: 80-95.
• Xu Z, Zhou G, Shimizu H. 2010. Plant responses to drought and rewatering. Plant Signal Behav 5: 649–54.