Introduction

Prolonged and intense drought periods are one of the consequences of ongoing climate change (IPCC 2007, 2014) as predicted by most climate change scenarios (Burke et al., 2006). Central Europe experienced extreme droughts during summers 2003, 2015 and 2018 (Ionita et al., 2017; Hänsel et al., 2019). The ramifications of such extreme events were drastic for temperate European (Ciais et al., 2005; Leuzinger et al., 2005) and North American forests (Asner et al., 2016; Hartmann et al., 2018). Long and severe drought periods often lead to a severe shortage of water for plants which may result in hydraulic failure, the collapse of the water conducting system, often resulting in tree death (Brodribb and Cochard, 2009; Urli et al., 2013). In particular trees as long-living organisms possess versatile strategies against drought such as hydraulic (Tomasella et al., 2017a) or photosynthetic acclimation (Watkinson et al., 2003). Another strategy is hydraulic redistribution (HR) of water from moist (e.g. deeper) to drier soil layers via the root system (Neumann and Cardon, 2012; Prieto et al., 2012), a phenomenon hardly explored for temperate forests (Emerman and Dawson, 1996). If deeper roots have access to more water-saturated soil layers, the complete root system will equilibrate at high water potentials, in particular during the night when stomata close. The water potential gradient within the soil is the driving factor for the redistribution of water towards the soil layers with lower water potential along the root. A wide range of plant species, including conifers and angiosperm trees, are able to redistribute water (e.g. Prieto et al., 2012; Hafner et al., 2017), while the amount of redistributed water can strongly vary (from 0.04 to 4 mm water per day) even within one ecosystem (Neumann and Cardon, 2012). Nevertheless, on average HR water can represent up to 15 % of water used for transpiration (Neumann and Cardon, 2012) or up to 80% of root water (Hafner et al., 2017) and therefore play an important role for the water balance of plants. Several empirical studies report a suit of factors that define the amount of HR and consequently are used in model predictions (Neumann and Cardon, 2012 and citations within). Among these are ‘external’ factors, such as the water potential gradient (Ryel et al., 2004) or root-soil contact and ‘internal’ driving factors, such as root conduit anatomy (Hafner et al., 2017). However, fine root anatomy and related hydraulic conductivities are hardly studied. Especially conductivity measurements of roots are scarce and in the reverse direction, i.e. from the rootstock to the fine roots as it is the case of HR, unreported.

In a conducting element, the diameter of the pipes is the most confining factor for the amount of transported water, as given by the law of Hagen-Poiseuille. Thus, roots with high water transport capacity should also redistribute more water. During HR water flows against the “usual” direction; nevertheless, we expect the conductivity of fine roots for water to be independent of its direction. To this end, we investigated the fine root systems of six temperate tree species, i.e. Norway spruce (Picea abies L. Karst), European beech (Fagus sylvatica L.), sycamore maple (Acer pseudoplatanus L.), sweet chestnut (Castanea sativa Mill.), English oak (Quercus robur L.) and Douglas fir (Pseudotsuga menziesii Mirb. Franco). We chose these species not only for their importance in forestry and natural forests stands, but also for their differences in anatomy. As spruce and Douglas fir are conifers, they have only tracheids as conductive elements. Among the four angiosperms, two species were stem-diffuse porous (beech and maple) and two had a ring porous stem anatomy (chestnut and oak). Hence, we examined a broad spectrum in conduit sizes and wood traits, which are controlled by genetic and environmental factors (Schreiber et al., 2015). To test whether root order has an influence on anatomy, we compared primary roots with older, secondary roots, hypothesizing that fine root anatomy is similar in primary and secondary roots (H1). Closely related to anatomy is the root conductivity for water. As the reverse flow of water in roots could be an important limitations for HR, we compared the conductivity of forward and reverse flow in secondary roots of the six study tree species. Based on the analogy between roots and pipes and the law of Hagen-Poiseuille we hypothesized that there is no difference between forward and reverse water flow in fine roots (H2).

Materials and Methods

Results

Anatomy of primary and secondary roots

For the two conifers, within and between, there was no difference in the hydraulic diameter (D_H) between primary and secondary roots (P = 0.86, overall mean: 10.9 ± 2.1 µm, figure 2). For all angiosperms, primary roots had significantly smaller D_H compared to secondary roots (P < 0.05, figure 2). Among angiosperms, D_H in primary roots did not differ (P = 0.47, overall mean 19.4 ± 4.9 µm) (figure 2). For secondary roots, angiosperms showed significant differences between the species (P < 0.01, figure 2), with chestnut (47.0 ± 14.0 µm) having the largest D_H, followed by oak (37.1 ± 3.2 µm) and maple (29.9 ± 2.7 µm) and beech (29.2 ± 3.5 µm) having the smallest D_H. Overall, angiosperms showed a significantly larger D_H than conifers for both root orders (P < 0.001, figure 2).

Figure 1: Examples of laser ablated cross-sections.

Save View full size Expand inline Collapse inline

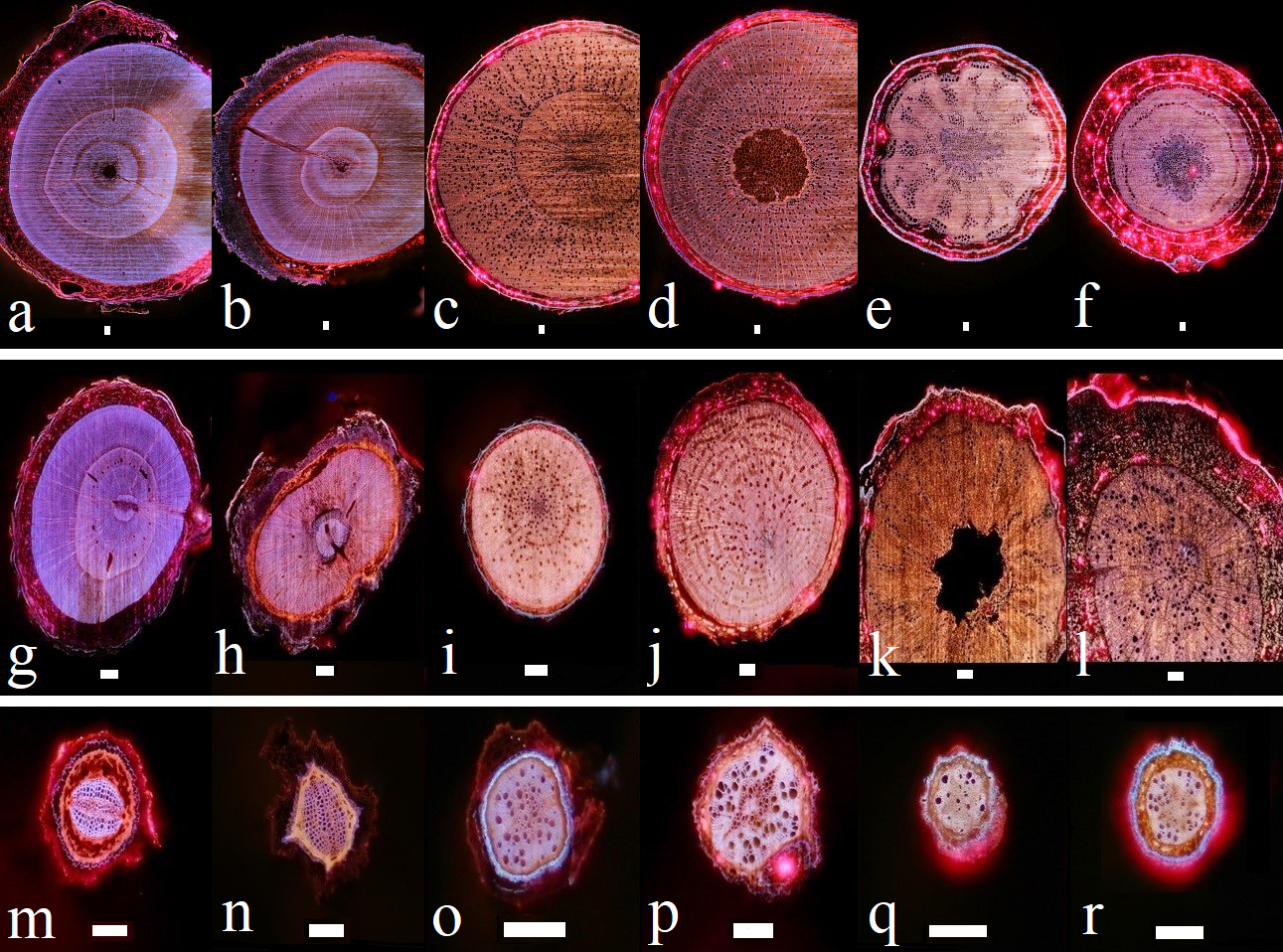
Laser ablated cross-sections of stem segments (upper row), secondary (middle row) and primary (lower row) roots of spruce (a, g & m), Douglas fir (b, h & n), beech (c, i & o), maple (d, j & p), oak (e, k & q) and chestnut (f, l & r). Bars represent 1000 µm for a-f and 100 µm for g-r.

The same pattern was found for the conduit diameter (D_, table 1). No differences in D were found for conifers, neither between root orders nor between the two species (table 1). Secondary roots in angiosperms showed on average 1.9 times larger D than primary roots (table 1). While no differences in D were found in primary roots between the angiosperm species (P > 0.05, table 1), in the secondary roots, chestnut showed significant larger D, than oak, being in between, and beech and maple showing the smallest D (table 1).     

Conduit density (C_D) of conifers was 17 times in primary and 32 times in secondary roots higher than of angiosperms (P < 0.001, table 1). While spruce tended to a higher C_D than Douglas fir, especially in primary roots, there was no intraspecific difference between primary and secondary roots within both species (table 1). For angiosperms, C_D was on average about five times higher in primary roots compared to secondary roots (P < 0.05, table1), however, no differences were found between the four species in each root order, respectively (table 1).

Figure 2: Mean hydraulic diameter per species

Save View full size Expand inline Collapse inline

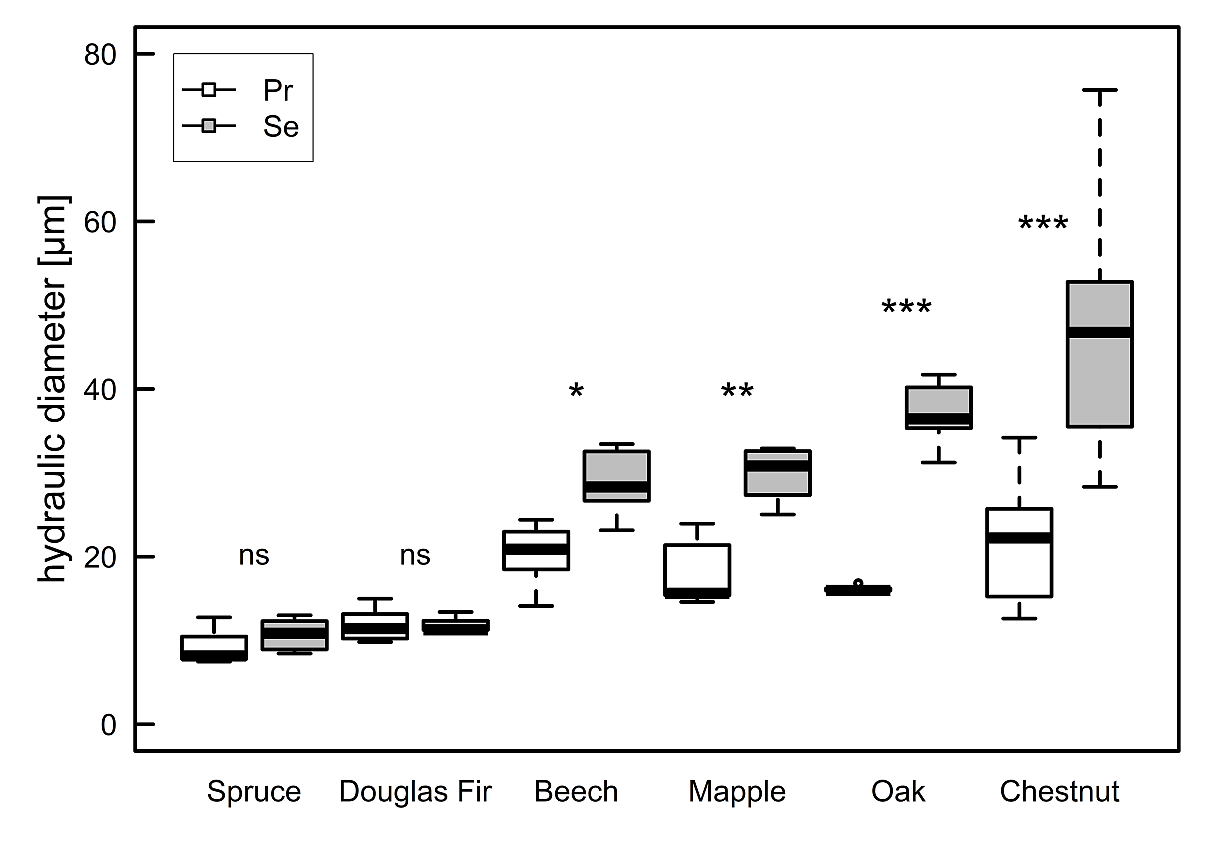
Hydraulic diameter (D_H) in primary roots (white) and secondary roots (grey); asterisks indicate significant differences within one species between primary and secondary roots (*** < 0.001, ** < 0.01, * < 0.05, ns > 0.05).

For the vessel lumen fraction (F) and the vessel composition index (S) a similar pattern was found. For both indices, no differences were found in primary roots within the four angiosperm and the two conifers, respectively (table 1). However, conifers tended to have double the amount of vessel lumen (F) (0.25 ± 0.07) than angiosperms (0.10 ± 0.05). In primary roots on the other hand, conifers (3.05E-8 ± 2.13E-8 mm⁴) had an almost sixty times lower vessel composition index (S) than angiosperms (1.76E-6 ± 1.21E-6 mm⁴). Overall, F for angiosperms was similar in primary roots (0.10 ± 0.05) compared to secondary roots (0.07 ± 0.03, table 1) and the same for conifers (0.25 ± 0.07 vs. 0.25 ± 0.07). For angiosperms, the vessel composition index (S) of secondary roots (2.06E-5 ± 3.12E-5 mm⁴) was on average about 19 times higher compared to primary roots (1.10E-6 ± 1.22E-6 mm⁴) (P <0.001, table 1), in particular in oak. Conversely, conifers showed very similar S in both root orders, but 37 times lower S in primary and 623 times lower S in secondary roots compared to angiosperms (table 1). Despite the high C_D in primary roots, only maple showed significant vessel grouping (V_G in table 1). In primary roots of maple, V_G was more prominent than in secondary roots (2.89 ± 0.33 to 2.01 ± 0.22, respectively). The three other angiosperms did not show any vessel grouping (table 1), neither in primary roots (1.09 ± 0.05) nor in secondary roots (1.11 ± 0.04).

Root hydraulic conductivity

The diameter of the root pieces used for forward (2.35 ± 0.95 mm) and reverse conductivity (2.36 ± 1.00 mm) did not show any significant difference. Both the flow direction and the plant species had a significant influence on the hydraulic conductivity (figure 3a). In forward direction, the species with the highest conductivity (k_{s_max_f}) was chestnut (2.39 ± 1.19 kg s^-1 m^-1 MPa^-1), followed by oak (2.05 ± 0.43 kg s^-1 m^-1 MPa^-1) and beech/ maple with similar values (1.35 ± 0.24 kg s^-1 m^-1 MPa^-1 and 1.21 ± 0.29 kg s^-1 m^-1 MPa^-1, respectively). Douglas fir and spruce had relatively low and similar values (0.32 ± 0.12 kg s^-1 m^-1 MPa^-1 and 0.28 ± 0.09 kg s^-1 m^-1 MPa^-1, respectively). The same pattern was found for the reverse direction (k_{s_max_r}, figure 3a). For the two conifers there was no difference between the forward and the reverse conductivity, whereas the four angiosperms showed a highly significant difference (figure 3a). The reverse conductivity was reduced by 39 ± 11 % compared to the forward conductivity in angiosperms, irrespective of species (figure 3b). Conversely, hydraulic conductivity in stems (k_{s_max_stem_f} and k_{s_max_stem_r}) of maple and oak was not different between forward and reverse direction (P = 0.30, figure 3c). Concurring with the results in the roots, oak had a higher conductivity in stems than maple in both directions (P < 0.001, figure 3c).

Table 1: Anatomical parameters

Save View full size Expand inline Collapse inline

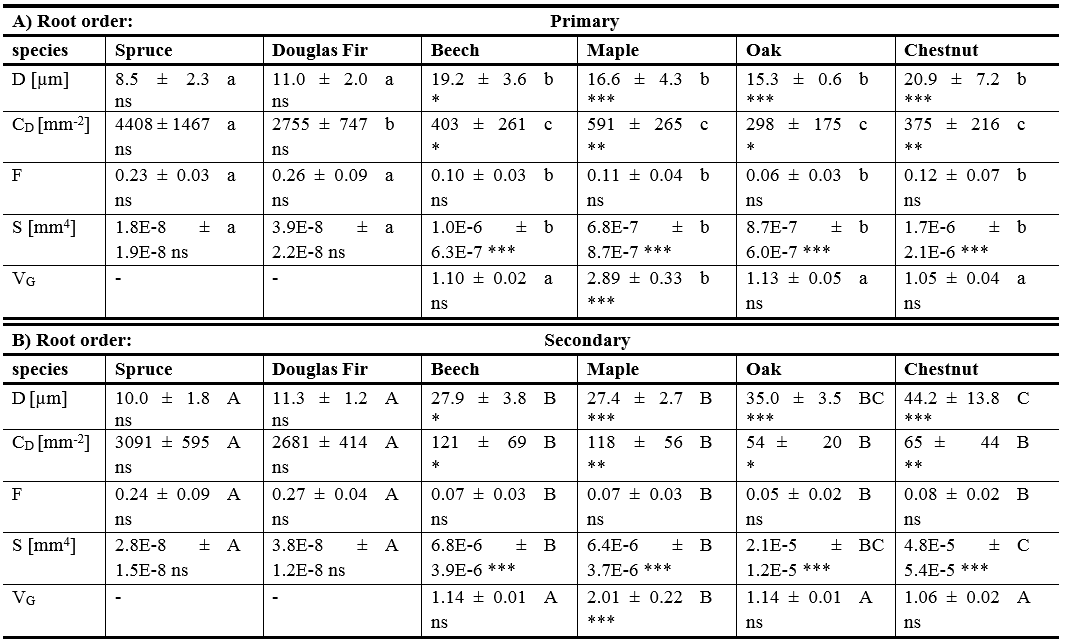
Anatomy parameters conduit diameter (D), conduit density (C_D), vessel lumen fraction (F), vessel composition index (S) and vessel grouping index (V_G) in primary (A) and secondary roots (B). Asterisks indicate significant differences within species between primary and secondary roots with *** < 0.001, ** < 0.01, * < 0.05 and ns > 0.05. Different letters indicate significant differences between species with small letters for primary roots and capital letters for secondary roots (values are given as the mean ± 1 SD).

Discussion

In this study, reverse conductivity in fine roots was systematically tested for the first time. Opposing to H1, differences in several anatomical parameters (e.g. D_H, C_D, S) were found between young, primary and older, secondary roots. Furthermore, we found differences in the magnitude between forward and reverse hydraulic conductivity in fine roots of angiosperms, contradicting H2. Reverse conductivity was reduced by about 40 % compared to the forward conductivity.

Root anatomy of primary and secondary roots

Roots with predominantly primary growth, showed different xylem anatomical structures compared to older, secondary roots. Additionally, primary roots of rather unrelated species (e.g. angiosperm genera) were anatomically rather similar. Conversely, for older, secondary roots, clear differences between species were found in D, D_H and S. For the two conifers, the conduit size was consistent for both root orders, which is contradictory to findings along the stem to branches, where conduit size is decreasing (McCulloh and Sperry, 2005; Woodruff et al., 2008). Therefore we accept H1 for the two conifer species. Additionally, anatomy of fine roots in conifers seems to be very similar to anatomy of twigs in many parameters (D and C_D, Tomasella et al., 2017a). For the four angiosperm species, on the other hand, we found distinct differences between the two root orders, showing that with increasing age, roots seem to change their xylem anatomy. Especially the increase in diameter and the decrease in density of water conducting conduits is obvious. We therefore reject H1 for the four angiosperm species.

Figure 3: Maximum specific hydraulic conductivity and loss of conductivity.

Save View full size Expand inline Collapse inline

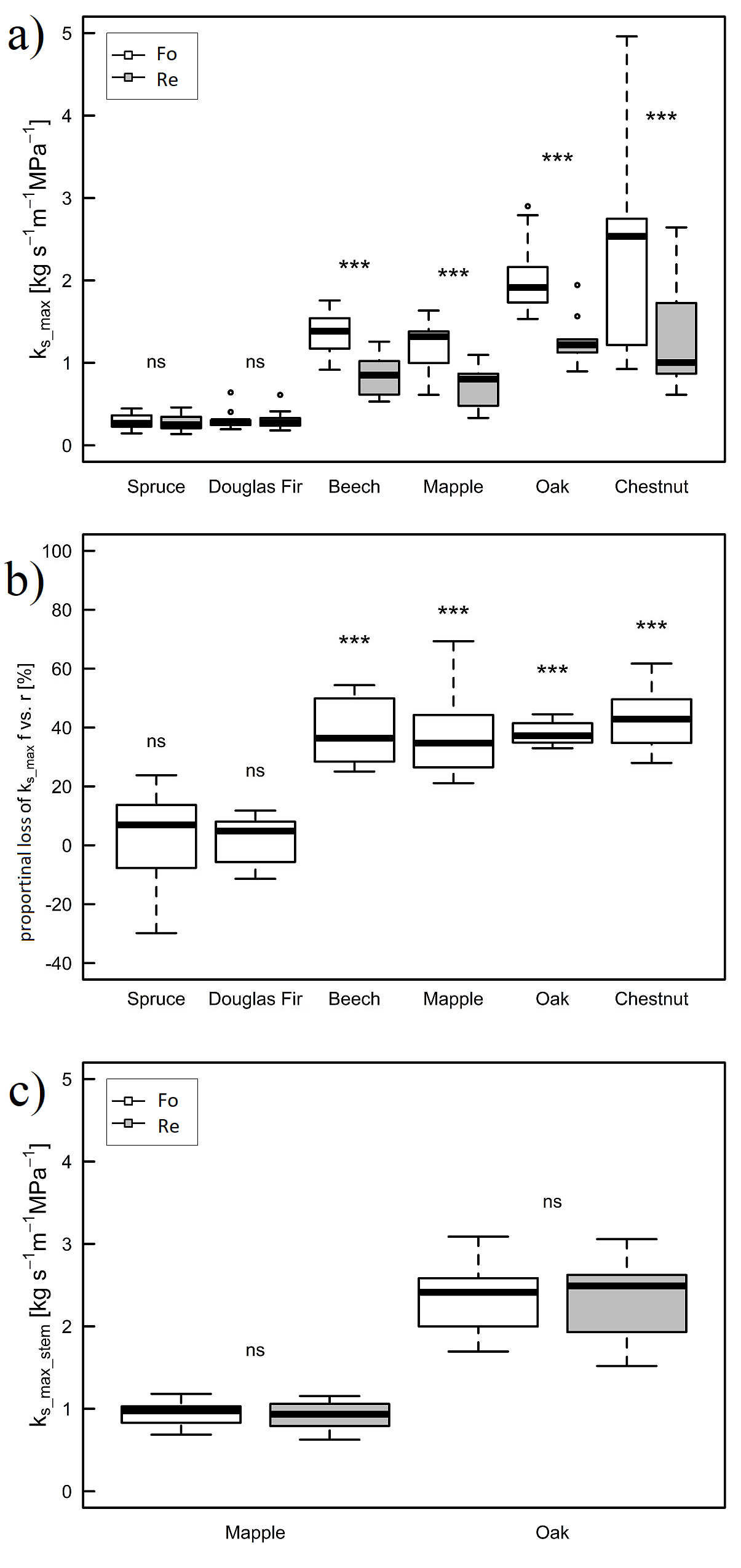
Maximum specific hydraulic forward (white) and reverse (grey) conductivity of roots (k_{s_max}, a), proportional loss of conductivity of the reverse direction compared to forward direction in roots (proportional loss of k_{s_max} f vs. r, b) and hydraulic maximum specific forward (white) and reverse (grey) conductivity of stems (k_{s_max_stem}, c). Asterisks indicate significant differences within one species between forward and reverse conductivity (3a & c). In 3b asterisks indicate significant differences to zero (*** < 0.001, ns > 0.05).

Whereas conifers seem to be very conservative in their anatomy, angiosperms tend to be more plastic. Over the four angiosperms, the two stem ring porous species (chestnut and oak) showed bigger vessels in the roots than the two stem diffuse-porous species (maple and beech), which is consistent with anatomical measurements of the stem (McCulloh et al. 2010). However, vessel distribution in all analyzed fine roots seemed more diffuse-porous, i.e. even distribution of similar-sized conduits over the whole year-ring, including chestnut and oak, which is in conflict with their vessel arrangement in stems (Barbaroux and Bréda, 2002; Fonti and Garcia-Gontález, 2004). This may be related to the longer growth period of roots, depending on water availability and soil temperature (Tryon and Chapin, 1983) with vessels being formed over the whole root growing season unlike stem growth peaking in early summer (McDougal, 1916; Alvarez-Uria and Körner, 2007). Vessel density also supports the diffuse porous anatomy of roots, as no differences were found among angiosperm species, neither in the primary nor in the secondary roots. Typical vessel densities in stems for ring-porous species are at 52 ± 17 mm^-2 (for 3-year-old oak from Steppe and Lemeur, 2007) and for diffuse-porous species at 872 ± 113 mm^-2 (beech twigs, Tomasella et al., 2017a). In the roots the four angiosperm species showed values in between with on average 417 mm^-2 in primary and 78 mm^-2 in secondary roots despite their consistent diffuse-porous distribution of vessels. The higher vessel density in primary roots emphasizes the importance of vessel structures for the water transport in angiosperms (Sperry, 2003). At the same time the high density of vessels is at the expense of mechanical strength, which is more important for stems and coarse roots (Preston et al., 2006), as they need to withstand harsh compressive stress during storms and snow load (James et al., 2006). Vessel lumen fraction (F) in stems of angiosperms is around 0.136 (Zanne et al., 2010) and similar to those in fine roots (0.083 for both ages). Therefore, roots seem to build xylem with a similar amount of conductive area as stems. Otherwise, the vessel composition index (S) for angiosperms in primary roots is about 90 times and in secondary roots 5 times lower compared to aboveground values (9.6E-5 mm⁴ from Zanne et al. (2010)). Hence, the conductive area in angiosperm roots is composed of more but smaller conduits than in stems (Zanne et al., 2010). According to the vessel composition index, roots seem to follow a more conservative strategy, reducing the risk of embolisms at the cost of a lower water transport (Zanne et al., 2010), with primary roots being even more conservative than secondary roots. However, as roots face very different environmental conditions than stems/twigs, the vessel composition index might not be a useful tool to predict cavitation resistance in roots, especially as our measured species are all mesophilous with similar cavitation resistances (P₅₀ of -2.2 MPa for Acer pseudoplatanus (Lens et al., 2011), -4.74 MPa for Quercus robur (Lobo et al., 2018) and -3.4 MPa for Fagus sylvatica (Tomasella et al., 2017a)). This could be an important issue under drought stress conditions, as hydraulic failure in the water up-taking organ would consequently kill the plant (Jackson et al., 2000). Therefore, the higher safety margin against embolisms in roots may be one strategy of plants to avoid hydraulic failure (Delzon and Cochard, 2014). Overall, stem anatomy is not a reliable proxy for root anatomy, especially for fine roots of angiosperms.

Reverse vs. forward hydraulic conductivity in roots

Direction of water flow in roots, i.e. forward or reverse, did not affect conductivity in conifer roots, yet for all angiosperms a 40 % reduction in the reverse compared to forward conductivity was found. Looking at the conductive system, the xylem, the main difference between the two groups are the existence of vessels, which are only in angiosperms (Lüttge et al., 2005). Hence, the anatomy/structure of vessel elements in angiosperm wood most likely plays a decisive role in the reduction of conductivity of reverse water flow. To our knowledge, only very few studies have dealt with vessel anatomy in detail. Deducted from this knowledge we identified four putative reasons for the conductivity reduction in reverse direction (figure 4).

Figure 4: Schematic figures for possible anatomical causes of reverse conductivity reduction

Save View full size Expand inline Collapse inline

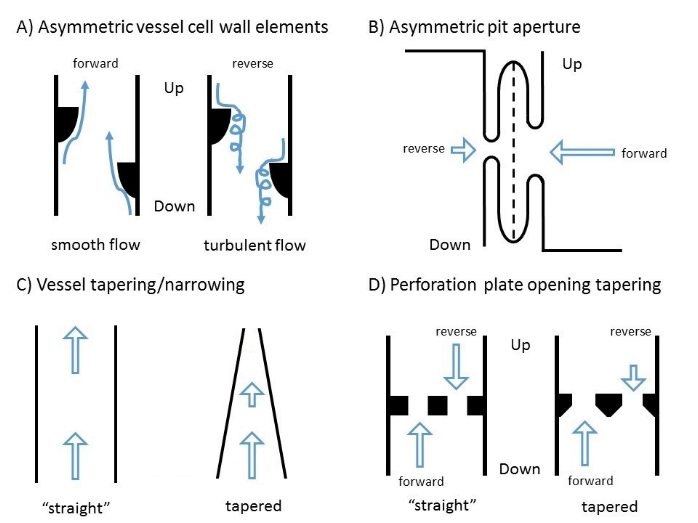
Schematic figures for possible anatomical causes of reverse conductivity reduction: A) asymmetric vessel cell wall elements (e.g. warts), B) Asymmetric pit aperture, C) tapering/narrowing of vessels and D) tapering of perforation plate openings (Arrows indicate flow direction and the length is indicating the magnitude of the conductivity).

a) Asymmetric vessel warts

Independent of the type of thickening, vessels have elements pointing into the lumen (e.g. warts, Bailey, 1944; Ohtani et al., 1983, Jansen et al., 1998), possibly causing some disturbances in the conductivity. If these elements were asymmetric, they could cause higher resistance and turbulences for one flow direction (figure 4 a). Such disturbances in the conductivity would then hinder the reverse flow (Karino et al., 1987). However, this would mean that the manner of secondary thickening of vessels and especially its remnants are different between root and stem xylem, as no difference was found in the conductivity for the stem xylem.

b) Asymmetric pit aperture

Pits and the connectivity between vessel elements are supposed to play an important role in safety and resistance for the hydraulic system of plants (Choat et al., 2008). If the pits opening would be smaller on one side, the conductivity could be reduced (figure 4 B). If the smaller opening would be consistently at the vessel side closer to the root tip, this could result in a reduction in the reverse conductivity (Steven Jansen, personal communication, figure 4 b). But as no reduction in the reverse conductivity was found in the stem segments, this would indicate, that pits of the stems are built differently from the pits in roots. Up to this point however, most studies about pits were made in aboveground organs (Choat et al., 2008 and citations within). However, it appears unlikely that the pits themselves are responsible for the reduction of reverse conductivity. First, pits in angiosperms are well studied (e.g. Choat et al., 2008) and so far there are no indications that they would favor one direction, as they have to “seal” either vessel in case of cavitation. Second, as the vessel grouping index (V_G) in the four angiosperm roots was diverse, with only maple showing a considerable amount of vessel grouping, it appears unlikely that reverse conductivity reduction is related to pits anatomy. Plants with a high vessel grouping index would be considered to have more connecting pits between the vessels than plants with a low vessel grouping index. Nevertheless, we saw no differences in the amount of conductivity reduction between maple with high and the other three angiosperms with lower V_G.

c) Vessel tapering

Another reason for the reduced conductivity along a conduit could be tapering towards one end (Petit et al. 2008). Vessel tapering is known to occur in stems and branches (Anfodillo et al., 2006; Petit et al., 2010) and is assumed to happen in roots (Enquist, 2003). As given by the law of Hagen-Poiseuille, the conductivity is dependent on the fourth power of the vessel radius (Sperry et al., 2006). Tapering of vessels towards the root tip would limit reverse flow compared to forward flow (Walander and Prasassarakich, 1976; Rubenstein et al., 2011). However, the reduction of reverse conductivity was only found in angiosperms, but tapering is known to happen in conifers too. Nevertheless, the degree of tapering may be related to the size of conduits and xylem dimension and may therefore be neglectable in tracheids and large diameter stems but not for vessels and small roots/twigs respectively.

d) Perforation/end plates

Perforation plates, i.e. the remnants of cell walls between connected vessels (Christman and Sperry, 2010), increase the resistance for water flow. While there are different forms, scalariform perforation plates are common in angiosperms (Ellerby and Ennos, 1998). If the openings in these plates would taper to one side (e.g. conical shaped), the resistance for one direction would increase (figure 4 d, Walander and Prasassarakich, 1976; Rubenstein et al., 2011). Again, this would imply a different structure and/or building process of root xylem compared to stem xylem, as no reduction of conductivity was found in stems.

As conifers showed no difference between the conductivity directions, H2 was accepted for them. For angiosperms, H2 was rejected, as a reduction of 40 % was found in the reverse conductivity compared to the forward conductivity. The four points mentioned above are based on the physical principles of resistance and turbulent flow, although flow rates under HR are relatively low compared to maximum forward flow and therefore the impact of turbulences might not be very big. None of them has been examined so far and will hopefully stimulate future work. However, reverse root conductivity seems to limit internal HR in angiosperm trees stronger than assumed (Neumann and Cardon, 2012). Transfer of water into the soil might be additionally limited as the conductance of the whole root system is additionally limited by other mechanisms such as forcing of water through the symplasm by the casparian stripe during water uptake or root suberization. The reduction in reverse conductivity in roots can also be interpreted from an evolutionary point of view. As HR is a passive phenomenon, trees reducing the loss of water into the soil to some extent may benefit during drought events and therefore may be favored during selection processes. As conifers only have tracheids, which conduct smaller amounts of water compared to vessels, the losses might be bearable anyway.

Acknowledgements

We thank Roman Meier, Peter Kuba and Thomas Feuerbach for the maintenance of the climate chambers and help during the setup of the experiment. We thank Dr. Marc Göbel (Cornell University) and Benjamin Hall and Dr. Asheesh Lanba of Lasers for Innovative Solutions (L4iS) for conducting laser ablation tomography. In addition, we want to thank Dr. Steven Jansen and Dr. Taryn Bauerle for stimulating discussions about the results of this study.

References

• Alvarez-Uria P., Körner C., 2007. Low temperature limits of root growth in deciduous and evergreen temperate tree species. Funct Ecol 21:211-218. https://doi.org/10.1111/j.1365-2435.2007.01231.x
• Anfodillo T., Carraro V., Carrer M., Fior C., Rossi S., 2006. Convergent tapering of xylem conduits in different woody species. New Phytol 169:279-290. https://doi.org/10.1111/j.1469-8137.2005.01587.x
• Asner G.P., Brodrick P.G., Anderson C.B., Vaughn N., Knapp D.E., Martin R.E., 2016. Progressive forest canopy water loss during the 2012-2015 California drought. Proc Natl Acad Sci 113: E249-E255. https://doi.org/10.1073/pnas.1523397113
• Bailey I.W., 1944. The Development of Vessels in Angiosperms and its Significance in Morphological Research. Am J Bot 31:421-428. https://doi.org/10.1002/j.1537-2197.1944.tb08053.x
• Barbaroux C., Bréda N., 2002. Contrasting distribution and seasonal dynamics of carbohydrate reserves in stem wood of adult ring-porous sessile oak and diffuse-porous beech trees.pdf. Tree Physiol 22:1201-1210. https://doi.org/10.1093/treephys/22.17.1201
• Barigah T.S., Charrier O., Douris M., Bonhomme M., Herbette S., Améglio T., Fichot R., Brignolas F., Cochard H., 2013. Water stress-induced xylem hydraulic failure is a causal factor of tree mortality in beech and poplar. Ann Bot 112:1431-1437. https://doi.org/10.1093/aob/mct204
• Brodribb T.J., Cochard H., 2009. Hydraulic Failure Defines the Recovery and Point of Death in Water-Stressed Conifers. Plant Physiol 149:575-584. https://doi.org/10.1104/pp.108.129783
• Burke E.J., Brown S.J., Christidis N., 2006. Modeling the Recent Evolution of Global Drought and Projections for the Twenty-First Century with the Hadley Centre Climate Model. J Hydrometeorol 7:1113-1125. https://doi.org/10.1175/JHM544.1
• Carlquist S., 2001. Comparative Wood Anatomy - Systematic, Ecological, and Evolutionary Aspects of Dicotyledon wood, 2nd edn. Springer Verlag, Berlin. https://doi.org/10.1007/978-3-662-04578-7
• Chimungu JG, Brown KM, Lynch JP (2014) Large Root Cortical Cell Size Improves Drought Tolerance in Maize. Plant Physiol 166:2166-2178. https://doi.org/10.1104/pp.114.250449
• Choat B, Cobb AR, Jansen S (2008) Structure and function of bordered pits: New discoveries and impacts on whole-plant hydraulic function. New Phytol 177:608-626. https://doi.org/10.1111/j.1469-8137.2007.02317.x
• Christman MA, Sperry JS (2010) Single-vessel flow measurements indicate scalariform perforation plates confer higher flow resistance than previously estimated. Plant, Cell Environ 33:431-443. https://doi.org/10.1111/j.1365-3040.2009.02094.x
• Ciais P, Reichstein M, Viovy N, Granier A, Ogée J, Allard V, Aubinet M, Buchmann N, Bernhofer C, Carrara A, Chevallier F, De Noblet N, Friend AD, Friedlingstein P, Grünwald T, Heinesch B, Keronen P, Knohl A, Krinner G, Loustau D, Manca G, Matteucci G, Miglietta F, Ourcival JM, Papale D, Pilegaard K, Rambal S, Seufert G, Soussana JF, Sanz MJ, Schulze ED, Vesala T, Valentini R (2005) Europe-wide reduction in primary productivity caused by the heat and drought in 2003. Nature 437:529-533. https://doi.org/10.1038/nature03972
• Cochard H, Badel E, Herbette S, Delzon S, Choat B, Jansen S (2013) Methods for measuring plant vulnerability to cavitation: A critical review. J Exp Bot 64:4779-4791. https://doi.org/10.1093/jxb/ert193
• Delzon S, Cochard H (2014) Recent advances in tree hydraulics highlight the ecological significance of the hydraulic safety margin. New Phytol 203:355-358. https://doi.org/10.1111/nph.12798
• Ellerby DJ, Ennos AR (1998) Resistances to fluid flow of model xylem vessels with simple and scalariform perforation plates. J Exp Bot 49:979-985. https://doi.org/10.1093/jxb/49.323.979
• Emerman SH, Dawson TE (2010) Hydraulic Lift and Its Influence on the Water Content of the Rhizosphere. Oecologia 108:273-278. https://doi.org/10.1007/BF00334651
• Enquist BJ (2003) Cope's rule and the evolution of long-distance transport in vascular plants: Allometric scaling, biomass partitioning and optimization. Plant, Cell Environ 26:151-161. https://doi.org/10.1046/j.1365-3040.2003.00987.x
• Fonti P, García-González I (2004) Suitability of chestnut earlywood vessel chronologies for ecological studies. New Phytol 163:77-86. https://doi.org/10.1111/j.1469-8137.2004.01089.x
• Hacke UG, Sperry JS, Feild TS, Sano Y, Sikkema EH, Pittermann J (2007) Water Transport in Vesselless Angiosperms: Conducting Efficiency and Cavitation Safety. Int J Plant Sci 168:1113-1126. https://doi.org/10.1086/520724
• Hänsel S, Ustrnul Z, Łupikasza E, Skalak P (2019) Assessing seasonal drought variations and trends over Central Europe. Adv Water Resour 127:53-75. https://doi.org/10.1016/j.advwatres.2019.03.005
• Hafner BD, Tomasella M, Häberle K, Goebel M, Matyssek R, Grams TEE (2017) Hydraulic redistribution under moderate drought among English oak, European beech and Norway spruce determined by deuterium isotope labeling in a split-root experiment. Tree Physiol:1-11. https://doi.org/10.1093/treephys/tpx050
• Hartmann H, Schuldt B, Sanders TGM, Macinnis-Ng C, Boehmer HJ, Allen CD, Bolte A, Crowther TW, Hansen MC, Medlyn BE, Ruehr NK, Anderegg WRL (2018) Monitoring global tree mortality patterns and trends. Report from the VW symposium 'Crossing scales and disciplines to identify global trends of tree mortality as indicators of forest health'. New Phytol 217:984-987. https://doi.org/10.1111/nph.14988
• Ionita, M., Tallaksen, L. M., Kingston, D. G., Stagge, J. H., Laaha, G., Van Lanen, H. A. J., Scholz, P., Chelcea, S. M. and Haslinger, K. (2017) The European 2015 drought from a climatological perspective, Hydrol. Earth Syst. Sci., 21, 1397-1419. https://doi.org/10.5194/hess-21-1397-2017
• IPCC, 2007: Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, M.L. Parry, O.F. Canziani, J.P. Palutikof, P.J. van der Linden and C.E. Hanson, Eds., Cambridge University Press, Cambridge, UK, 976pp.
• IPCC, 2014: Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Core Writing Team, R.K. Pachauri and L.A. Meyer (eds.)]. IPCC, Geneva, Switzerland, 151 pp.
• Jackson RB, Sperry JS, Dawson TE (2000) Root water uptake and transport: Using physiological processes in global predictions. Trends Plant Sci 5:482-488. https://doi.org/10.1016/S1360-1385(00)01766-0
• Jacobsen AL, Ewers FW, Pratt RB, Paddock III WA, Davis SD (2005) Do Xylem Fibers Affect Vessel Cavitation Resistance? Plant Physiol 139:546-556. https://doi.org/10.1104/pp.104.058404
• James KR, Haritos N, Ades PK (2006) Mechanical stability of trees under dynamic loads. Am J Bot 93:1522-1530. https://doi.org/10.3732/ajb.93.10.1522
• Jansen S, Smets E, Baas P (1998) Vestures in woody plants: A review. IAWA J 19:347-382. https://doi.org/10.1163/22941932-90000658
• Karino T, Goldsmith HL, Motomiya M, Mabuchi S, Sohara Y (1987) Flow Patterns in Vessels of Simple and Complex Geometriesa. Ann N Y Acad Sci 516:422-441. https://doi.org/10.1111/j.1749-6632.1987.tb33063.x
• Lens F, Sperry JS, Christman MA, Choat B, Rabaey D, Jansen S (2011) Testing hypotheses that link wood anatomy to cavitation resistance and hydraulic conductivity in the genus Acer. New Phytol 190:709-723. https://doi.org/10.1111/j.1469-8137.2010.03518.x
• Leuzinger S, Zotz G, Asshoff R, Korner C (2005) Responses of deciduous forest trees to severe drought in Central Europe. Tree Physiol 25:641-650. https://doi.org/10.1093/treephys/25.6.641
• Lobo A, Hansen JK, Kjær ED, Torres-Ruiz JM, Burlett R, Lemaire C, Parise C, Francioni C, Truffaut L, Kremer A, Tomášková I, Delzon S (2018) Assessing inter- and intraspecific variability of xylem vulnerability to embolism in oaks. For Ecol Manage 424:53-61. https://doi.org/10.1016/j.foreco.2018.04.031
• Lüttge U, Kluge M, Bauer G (2005) Botanik, 5th edn. WILEY-VCH Verlag, Weinheim.
• McCulloh KA, Sperry JS (2005) Patterns in hydraulic architecture and their implications for transport efficiency. Tree Physiol 25:257-67. https://doi.org/10.1093/treephys/25.3.257
• McCulloh K, Sperry JS, Lachenbruch B, Meinzer FC, Reich PB, Voelker S (2010) Moving water well: Comparing hydraulic efficiency in twigs and trunks of coniferous, ring-porous, and diffuse-porous saplings from temperate and tropical forests. New Phytol 186:439-450. https://doi.org/10.1111/j.1469-8137.2010.03181.x
• McDougall WB (1916) The Growth of Forest Tree Roots. Am J Bot 3:384-392. https://doi.org/10.1002/j.1537-2197.1916.tb05420.x
• Neumann RB, Gardon ZG (2012) The magnitude of hydraulic redistribution by plant roots: a review and synthesis of empirical and modeling studies. New Phytol 194:337-352. https://doi.org/10.1111/j.1469-8137.2012.04088.x
• Ohtani J, Meylan BA, Butterfield BG (1983) Occurrence of warts in the vessel elements and fibres of new zealand woods. New Zeal J Bot 21:359-372. https://doi.org/10.1080/0028825X.1983.10428568
• Petit G, Anfodillo T, Mencuccini M (2008) Tapering of xylem conduits and hydraulic limitations in sycamore (Acer pseudoplatanus) trees. New Phytol 177:653-664. https://doi.org/10.1111/j.1469-8137.2007.02291.x
• Petit G, Pfautsch S, Anfodillo T, Adams MA (2010) The challenge of tree height in Eucalyptus regnans: When xylem tapering overcomes hydraulic resistance. New Phytol 187:1146-1153. https://doi.org/10.1111/j.1469-8137.2010.03304.x
• Preston KA, Cornwell WK, DeNoyer JL (2006) Wood density and vessel traits as distinct correlates of ecological strategy in 51 California coast range angiosperms. New Phytol 170:807-818. https://doi.org/10.1111/j.1469-8137.2006.01712.x
• Prieto I, Armas C, Pugnaire FI (2012) Water release through plant roots: New insights into its consequences at the plant and ecosystem level. New Phytol 193:830-841. https://doi.org/10.1111/j.1469-8137.2011.04039.x
• R Development Core Team (2008) R: A language and environment for statistical computing. http://wwwR-project.org
• RStudio Team (2015) RStudio: Integrated Development for R. http://www.rstudio.com/
• Rubenstein DA, Yin W, Frame MD (2011) Biofluid Mechanics: An Introduction to Fluid Mechanics, Macrocirculation, and Microcirculation, 1st edn. Academic Press, Oxford.
• Ryel R.J. (2004) Hydraulic Redistribution. In: Esser K., Lüttge U., Beyschlag W., Murata J. (eds) Progress in Botany. Progress in Botany, vol 65. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-18819-0_17
• Scholz A, Klepsch M, Karimi Z, Jansen S (2013) How to quantify conduits in wood? Front Plant Sci 4:1-11. https://doi.org/10.3389/fpls.2013.00056
• Schreiber SG, Hacke UG, Hamann A (2015) Variation of xylem vessel diameters across a climate gradient: Insight from a reciprocal transplant experiment with a widespread boreal tree. Funct Ecol 29:1392-1401. https://doi.org/10.1111/1365-2435.12455
• Sperry JS (2003) Evolution of Water Transport and Xylem Structure. Int J Plant Sci 164: S115-S127. https://doi.org/10.1086/368398
• Sperry JS, Hacke UG, Pittermann J (2006) Size and function in conifer tracheids and angiosperm vessels. Am J Bot 93:1490-1500. https://doi.org/10.3732/ajb.93.10.1490
• Steppe K, Lemeur R (2007) Effects of ring-porous and diffuse-porous stem wood a natomy on the hydraulic parameters used in a water flow and storage model. Tree Physiol 27:43-52. https://doi.org/10.1093/treephys/27.1.43
• Tomasella M, Beikircher B, Häberle K-H, Hesse B, Kallenbach C, Matyssek R, Mayr S (2017a) Acclimation of branch and leaf hydraulics in adult Fagus sylvatica and Picea abies in a forest through-fall exclusion experiment. Tree Physiol:1-14. https://doi.org/10.1093/treephys/tpx140
• Tomasella M, Häberle K-H, Nardini A, Hesse B, Machlet A, Matyssek R (2017b) Post-drought hydraulic recovery is accompanied by non-structural carbohydrate depletion in the stem wood of Norway spruce saplings. Sci Rep 7:14308. https://doi.org/10.1038/s41598-017-14645-w
• Tyree, M. T. & Zimmermann, M. H. (2002). Xylem Structure and the Ascent of Sap. 2nd Edn. Berlin, Heidelberg, New York: Springer- Verlag https://doi.org/10.1007/978-3-662-04931-0
• Tryon PR, Chapin III FS (1983) Temperature control over root growth and root biomass in taiga forest trees. Can J For Res 13:827-833. https://doi.org/10.1139/x83-112
• Urli M, Porté AJ, Cochard H, Guengant Y, Burlett R, Delzon S (2013) Xylem embolism threshold for catastrophic hydraulic failure in angiosperm trees. Tree Physiol 33:672-683. https://doi.org/10.1093/treephys/tpt030
• Walawender W, Prasassarakich P (1976) Flow in Tapering and Cylindrical Vessels. Microvasc Res 12:1-12. https://doi.org/10.1016/0026-2862(76)90002-9
• Watkinson JI, Sioson AA, Vasquez-Robinet C, Shukla M, Kumar D, Ellis M, Heath LS, Ramakrishan N, Chevone B, Watson L. T, van Zyl L, Egertsdotter U, Sederoff RR, Grene R (2003) Photosynthetic Acclimation Is Reflected in Specific Patterns of Gene Expression in Drought-Stressed Loblolly Pine. Plant Physiol 133:1702-1716. https://doi.org/10.1104/pp.103.026914
• Woodruff DR, Meinzer FC, Lachenbruch B (2008) Height-related trends in leaf xylem anatomy and shoot hydraulic characteristics in a tall conifer: Safety versus efficiency in water transport. New Phytol 180:90-99. https://doi.org/10.1111/j.1469-8137.2008.02551.x
• Zanne AE, Westoby M, Falster DS, Ackerly DD, Loarie SR, Arnold SEJ, Coomes DA (2010) Angiosperm wood structure: Global patterns in vessel anatomy and their relation to wood density and potential conductivity. Am J Bot 97:207-215. https://doi.org/10.3732/ajb.0900178