Introduction

Cavitation refers to ‘the nucleation and growth of a bubble filled with gas and vapor within a liquid due to supersaturation and superheat' (Stroock et al., 2014). In plants, cavitation manifests as the disruption of water columns in plant vessels or tracheids caused by the formation of water vapor and air bubbles due to high negative xylem water potential resulting from low soil water availability and/or high atmospheric water demand (Schönbeck et al., 2022). The expansion of bubbles in conduits blocks sap flow, which leads to the embolization of the elements and the inability to transport water. As the xylem pressure potential becomes more negative (i.e., increase of xylem tension), the embolism spreads from one conduit element to another (Sperry and Tyree, 1988). The relationship between the percent loss of hydraulic conductivity and the xylem water tension is known as a vulnerability curve (VC). Determining the parameters from this curve, including the water potentials inducing 12, 50 and 88% of embolism (hereafter respectively P₁₂, P₅₀ and P₈₈) and the slope at P₅₀ (S₅₀) permits a quantitative assessment of resistance to cavitation.

These VC parameters are functional traits of the xylem that are strongly linked to survival, as hydraulic failure is a critical mechanism of drought-induced mortality (Anderegg et al., 2015; McDowell et al., 2022). Therefore, they are widely used to determine hydraulic safety margins, a standard metric for assessing tree vulnerability to drought (Choat et al., 2012; Delzon and Cochard, 2014; Chen et al., 2022). Hydraulic safety margins are defined as the difference between P₁₂, P₅₀ or P₈₈ and the observed seasonal minimal water potential (Meinzer et al., 2009). Incorporating hydraulic traits, such as VC parameters, could significantly enhance the ability of models to predict tree survival in the context of climate change (Anderegg et al., 2016; Choat et al., 2018). Vulnerability to cavitation is one of several relevant functional traits that can be used together to compare the sensitivity of different tree species to drought. This information is essential for practitioners and policymakers to adapt silvicultural practices and, more generally, forest management to future climate (Boisvert‐Marsh et al., 2020).

The mechanism of hydraulic failure currently holds the most potential for modelling the processes that drive drought-induced mortality (Choat et al., 2018). However, a recent study by Venturas et al. (2021) showed that the modelled percent loss of conductivity did not substantially contribute to explained variance at landscape scales, even though it was a significant predictor of mortality. Different explanations have been put forward as to why modelled hydraulic stress alone does not better explain drought-induced mortality (Rowland et al., 2021; Venturas et al., 2021). For instance, some trees could be more or less vulnerable than a tree represented by the mean curve. Therefore, the modelled tree may not exceed any critical threshold, and the risk of mortality is underestimated. Furthermore, the value of a hydraulic failure threshold is still debated (Brodribb and Cochard, 2009; Urli et al., 2013; Adams et al., 2017; Liang et al., 2021) with some trees surviving to a PLC>90% (Hammond et al., 2019). Other mechanisms that contribute to tree death include carbon starvation, phloem transport failure, symplastic failure of meristem (Mencuccini et al., 2015; Mantova et al., 2021; Hajek et al., 2022), level of isohydry, biomass portioning, and the critical water content of different organs (Martínez-Vilalta et al., 2019), should be considered in this model to better predict the sensitivity of forests to upcoming droughts (Skelton et al., 2015). The same problem as for mortality prediction was observed when sorting species according to their sensitivity to climate without considering the error around the mean curve or the mean value of P₅₀. This could lead to counterproductive decisions in species selection when trying to adapt forests to climate change. Therefore, it is crucial to better report the confidence interval around VC parameters in scientific studies, in order to include the variability around VC more effectively in predictive models or in the decision-making process.

Various methods can be used to construct vulnerability curves, and we assert that these methods are a primary source of variability because different artifacts are associated with each approach, which Cochard et al. (2013) and Venturas et al. (2017) thoroughly reviewed. For example, different methods may produce different curves for a given species. The VC parameters have been compared across methods in various studies for different species (e.g., Venturas et al., 2019; Sergent et al., 2020). In this study, we constructed VCs for four conifer species: black spruce (Picea mariana (Miller) Britton, Stern & Poggenburgh), white spruce (Picea glauca (Moench) Voss), Norway spruce (Picea abies (Linnaeus) H. Karsten), and Eastern white pine (Pinus strobus Linnaeus) using three different methods. First, we used the air injection method by pressure sleeve, which involves injecting air with positive pressure into a pressure sleeve chamber containing a sample with its two ends protruding out of the chamber. We chose this method because it is increasingly used to build VCs, easy to implement, and relatively inexpensive compared to other methods for conifer species (Ennajeh et al., 2011; Venturas et al., 2017). Then, we compared the results obtained using this method with those measured using the two other methods: the pot and bench dehydration methods on intact seedlings in pots and twigs cut from intact seedlings in lab, respectively. These methods are time-consuming but considered to better simulate the natural process of dehydration under drought conditions (Cochard et al., 2013). We followed the best practices for testing these different methods (Melcher et al., 2012; Jansen et al., 2015): we used plant material of the same age, similar size, and same provenances, and used the same perfusing solution for the three methods (see the Materials and Methods section for more details). We determined the confidence interval of each VC using new code adapted from the fitplc package (Duursma and Choat, 2017); we hence obtained bootstrapped confidence intervals including individuals as a random variable for the air injection method. Finally, we compared the P₅₀ value determined in our experiments with those reported in the literature.

Materials and methods

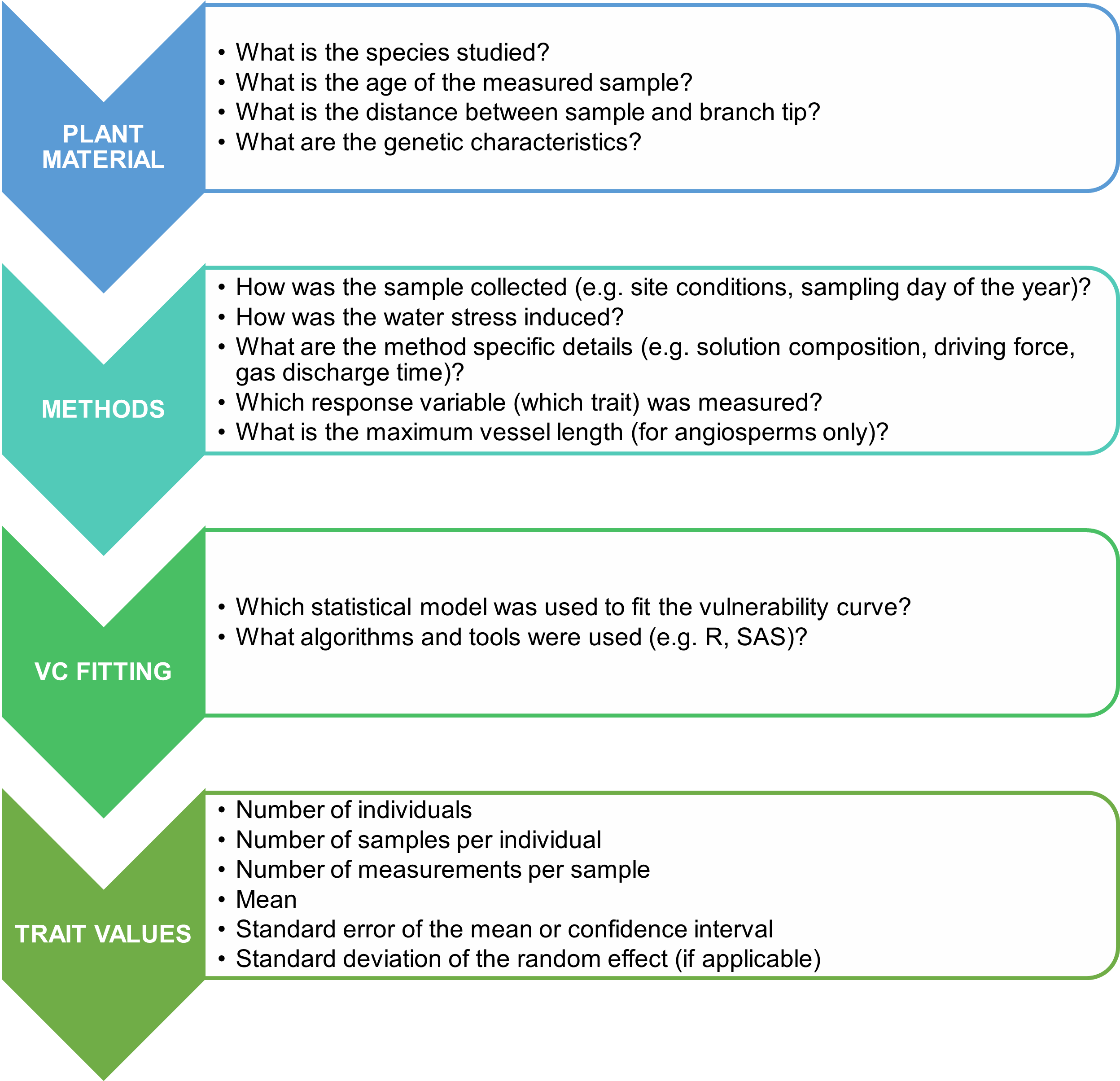
Plant material

We compared methods for building VCs on seedlings of four gymnosperm tree species: P. glauca, P. mariana P. abies and P. strobus. For each species, the seedlings were from the same genetic provenance adapted to the Outaouais ecological region of southern Québec, Canada, which is dominated by sugar maple (Acer saccharum Marshall) - yellow birch (Betula alleghaniensis Britton) forests. All seedlings for each species came from a single seed orchard at 46° 02' N, 73° 11' W (P. glauca), 46° 41' N, 72° 40' W (P. mariana), 45° 41′ N, 73° 19′ W (P. strobus), and 48° 21′ N, 72° 13′ W (P. abies).

For each species and method, we transplanted two-year old nursery-grown seedlings into 3.53 L cylindrical plastic pots (Classic Nursery Pot – 300 Series) that were filled with a mixture of peat moss, fine perlite, and vermiculite in a ratio of 3:1:1 (v:v:v). During the transplantation, we fertilized the seedlings with 15 g of slow-release fertilizer (ACER®nt 13-10-15). To prevent water evaporation, we covered the soil surface with silica. Seedlings were watered several times per week from the day of transplantation until the day before the experiment began, to keep soil water content at pot capacity. While the plant material was similar among all methods used to build VCs, the measurements for the pot dehydration and the air injection methods were conducted during summer of 2020, and those for the bench dehydration method were conducted in summer of 2021.

Hydraulic conductivity measurements

We measured the stem-specific hydraulic conductivity (K_s, kg m^-1 s^-1 MPa^-1) of a debarked part of the main stem (hereafter called stem segment) using a custom-built flow-meter following the protocol of Sack et al. (2011). The stem segment was cleaned with a 70% alcohol solution and cut about 4 cm from the base of the main stem axis. We used degassed, filtered (0.45 µm) distilled and purified (Barnstead E-Pure; Thermo Scientific, Waltham, MA, USA) water containing KCl (10 mM) and CaCl₂ (1 mM) as a perfusing solution. We used a tube of known hydraulic resistance (cf. Melcher et al. (2012) for more details) to measure the drop in pressure across, which allowed us to determine the flow rate through the stem segment (Q, kg s^-1). K_s was calculated using the following equation:

Ks = Q∆P × LAs

where ΔP (MPa) is the pressure gradient along the stem segment, L (m) its length and A_s (m²) is its cross-sectional area, calculated from the mean of the diameter measurements at each end of the stem segment. The pressure gradient was created using a hydraulic head with a range of 2 to 3 kPa. Each flow measurement was the average of 5-second measurements during the last 5 minutes of steady-state flow (i.e., when variation coefficient of flow was < 0.05) and then standardized to 25 °C.

Pot dehydration

Drought was induced by withholding water; seedlings were placed in different environments (laboratory or greenhouse) to induce different levels of dehydration. The experiment ended when measurements of water potential became impossible due to needle desiccation. The end of the experiment varied with species. We measured midday water potential (ψ, MPa) regularly throughout the dehydration using a Scholander pressure chamber (Model 1505-EXP, PMS Instrument Company, Albany, OR, USA) on twigs (stem + needles) of seedlings for Picea species (due to the small size of their needles) and on needles for P. strobus. All ψ measurements were made on twigs or needles from the previous growing season. To equilibrate ψ between measured needles and their associated twig, needles of P. strobus were placed inside foil bags at least 30 minutes before ψ measurements. Seedlings were exposed to controlled light (SK602GH, Spectrum King Grow Lights, Los Angeles, CA, USA) for at least 45 min (PPFD ~ 580 µmol m^-2 s^-1 at mid-seedling height) before ψ measurements. After each ψ measurement, seedlings were placed in a dark room.

On the following day, we cut a stem segment of approximately 10-12 cm stem segment from the main stem’s base. After removing the bark and cleaning the segment with a 70 % alcohol solution, we wrapped a subsample of approximately 4 cm in length with Parafilm and cut it under water (i.e., the perfusing solution) at the center of the stem segment. We then inserted it into the tube connected to the flow-meter apparatus and measured K_s using the procedures described earlier.

Bench dehydration

Following the protocol of Choat et al. (2015), seedlings were cut at the base of the main stem and air-dried on a bench in the laboratory for periods up to 140 h to achieve a wide range of xylem water potentials. After at least one hour in a dark environment to allow xylem pressure to equilibrate across the branch, water potentials were measured on 2 to 4 twigs of Picea seedlings and on needles for P. strobus. Twigs and needles were enclosed in foil bags before measurements were taken. Branches were removed from the main stem. The main stem was debarked and cleaned with 70 % alcohol, and its center was wrapped up with Parafilm. A subsample of 10-12 cm in length was then cut under water (i.e., the perfusing solution) from the base of the main stem. After a few minutes, another subsample of approximately 4 cm was cut under water at the center of the previous subsample and inserted into the tube connected to the flow-meter apparatus. K_s was measured using the previously described procedures.

Air injection by pressure collar sleeve

A stem segment of 20-25 cm in length was cut under water from the main stem of a seedling. The stem was debarked and perfused under vacuum in degassed, filtered (0.45 µm) distilled and purified water (Barnstead E-Pure; Thermo Scientific, Waltham, MA, USA) containing KCl (10 mM) and CaCl₂ (1 mM). After 24 h in the vacuum, a final cut was made in the perfusing solution to obtain a 15 cm stem segment. If no holes caused by the insertion of side branches were visible, notches were made on this new stem segment. The stem segment was then inserted into a double-ended pressure collar sleeve (PMS Instrument Company, Albany, OR, USA) that remained submerged in the perfusing solution throughout the experiment. The stem segment was connected to the flow-meter during K_s measurements and disconnected during air injection. A first stem-specific hydraulic conductivity measurement was taken before applying air injection inside the pressure collar sleeve. After that, the pressure in the collar sleeve was gradually increased in steps of 0.5 or 1.0 MPa to a maximum of 8 MPa. For each step, the exposure to pressure was for one minute and the duration of xylem pressure relaxation (no bubble seen at stem segment extremities) ranged between 15 min and 3 hours. K_s was measured after xylem relaxation following each applied pressure. This method allowed the construction of a VC per seedling, unlike the dehydration methods that require several seedlings to build a VC.

Fitting of vulnerability curves

For the three methods, VCs were fitted to the relationship between percent loss of conductivity (PLC, %) and the positive value of water potential for the dehydration methods or the applied pressure for the air injection method (P, MPa) using the fitplc package’s fitplc function (Duursma and Choat, 2017). PLC was calculated as follows:

PLC= 1- KsKs-max ×100

where K_s is the stem-specific hydraulic conductivity (kg m^-1 s^-1 Mpa^-1) and K_s-max is the maximum K_s defined as the measured K_s between -1 and 0 MPa, because the seedlings were grown under well-watered conditions before the beginning of the experiment for the pot and bench dehydration methods, or as the maximum value between K_s measured before the application of air injection (and after rehydration under vacuum) or for an applied pressure 1 MPa for the pressure collar air injection method. All VCs were fitted with a Weibull function, reparameterized by Ogle et al. (2009). VC parameters, P₁₂, P₅₀, and P₈₈, and their bootstrapped 95 % confidence intervals, were extracted using the fitplc package (Duursma and Choat, 2017) in R version 4.0.2 (R Core Team, 2020). The Weibull function is given by:

KsKs-max=1- x100PPxPxSxV


V= 1-x log1-x100

where P is a positive value of water potential or the applied pressure (MPa), P_x is P at which x% of conductivity is lost, S_x is the derivative (% MPa-1) at x (and therefore the slope of VC at P_x). x was fixed at 50 to fit the VCs because the curve fitting is more robust when x=50 (Duursma, 2018). Thus, P₁₂ and P₈₈ were extracted with the getPx function of the fitplc package. However, the fitplc package does not allow obtaining the bootstrapped 95 % confidence intervals around the VC when a random effect is added to the model. Therefore, we modified the code of the fitplc function to add ‘seedling ID’ as random effect in the Weibull model for the pressure collar air injection method. The code is available in the Supplementary materials.

Statistical analyses

We considered significant differences in the VC parameters when the bootstrapped 95% confidence intervals of VCs (P₁₂, P₅₀ and P₈₈) between 2 VCs did not overlap, following the approach of Duursma and Choat (2017). To test for significant effects of methods on maximum stem-specific hydraulic conductivity, we performed analyses of variance and post-hoc tests using the emmeans package (Lenth, 2021) in R version 4.0.2 (R Core Team, 2020).

Meta-analysis on P₅₀

We extracted P₅₀ values from the literature (peer-reviewed articles, Master's theses and Ph.D. theses) for six species: P. glauca, P. mariana, P. abies, P. strobus, Acer saccharum Marshall, and Quercus rubra Linnaeus. In this study, we present the results of four gymnosperm species that we studied. We performed four searches, one for each genus (Picea, Pinus, Acer and Quercus), on all databases (1900-2020) of the Web of Science database on July 14^th, 2020. For each search, the species names were searched using the genera in Latin and English and the Latin names not containing the genera (e.g., pinus OR pine OR “Strobus strobus” for P. strobus) using the Database of Canadian Vascular Plants (VASCAN; http://data.canadensys.net/vascan/ [Accessed July, 9 2020]). For each search, the terms related to the vulnerability to cavitation were as follows: (xylem AND embolism) OR (xylem AND cavitation) OR “percent loss of conduct*” OR “vulnerability curve” OR P50 OR “hydraulic conduct*” OR (“water transport” AND failure) OR (hydraulic AND failure) OR (“water transport” AND dysfunction) OR (hydraulic AND dysfunction). These terms were evaluated after different scoping searches. We also consulted the TOPIC database (Aubin et al., 2012) for each species. The results from TOPIC and from the four searches were combined, and duplicate results were removed (Figure 1).

During the title and the abstract screening and full-text assessment, we excluded studies that measured vulnerability to cavitation in organs other than stems or branches (such as leaves, roots or wood beams) or at the tissue level (inside a vessel), as well as studies related to winter embolism (unless they included a VC without winter embolism as a control), and studies in which embolism was calculated or modelled from sap flux. We only selected studies that were available in English or French.

To find primary sources of data, we noted literature review and meta-analysis articles containing VCs or P₅₀ of the studied species and searched their bibliographies. For each selected study, we extracted the following information when available for the qualitative analysis (Figure 1, Table S1): species, tree age, sample age, sample conditions, method to induce embolism, method to remove embolism (to determine K_s-max), model used for the VC fitting, VC parameters values and their errors, and maximum specific hydraulic conductivity (Table S1). We excluded data concerning levels of treatments (i.e., stems subjected/exposed to heat or freeze-thaw cycles) different from control levels, and added information about factors other than experimental treatments, such as altitude, population, etc. We extracted VC parameters values from primary sources (text, tables or figures) except when more detailed values and errors were provided in the secondary source. We eliminated articles on A. saccharum and Q. rubra, and those with VC built using the acoustic method during the selection of studies for the quantitative analysis. For each extracted P₅₀, we determined the confidence interval around P₅₀ when possible, using available information about the error around the mean (standard error, standard deviation, variation coefficient). Finally, we calculated the mean P₅₀ of P. strobus and its confidence interval by extracting the P₅₀ value of each measured branch in the study of .

We obtained 76 P₅₀ values by adding our own dataset, of which only 33 had associated information on the variation around the mean (standard deviation) or on the uncertainty on the mean (confidence interval for the mean or standard error) and the number of measurements used to construct the VC (Figure 3). Among these 33 values, 30 were related to P. abies. We performed an analysis of variance (ANOVA) on the P. abies dataset to test the effect of the method used to induce embolism (dehydration methods, centrifuge methods, and air injection methods) on P₅₀, using a linear mixed-effects model (LMM) with ‘study identifier' as random effect. We added a weight to the observations defined as the inverse of the variance. To confirm the results of this analysis on the other species, we used ANOVA to examine the response of P₅₀ to the method used to induce embolism, species and the two-way interaction on all species. We conducted the analysis using a linear model (LM). We performed post-hoc multiple mean comparisons using the Bonferroni test. For all the analyses, we conducted standard procedures for model diagnostics. We used R version 4.0.2 (R Core Team, 2020) for all analyses, along with the stats package for LM, the nlme package for LMM (Pinheiro et al., 2023) respectively, and the emmeans package (Lenth, 2021) for post-hoc tests.

Figure 1 PRISMA flow diagram illustrating the article selection process for the quantitative analyses.

Save View full size Expand inline Collapse inline

We extracted P₅₀ values of six species (P. glauca, P. mariana, P. abies, P. strobus, A. saccharum, Q. rubra) from peer-reviewed articles, Master’s theses and Ph.D. theses. Here, we present the results for the four studied gymnosperm species. Articles concerning A. saccharum and Q. rubra, as well as those with VC built using the acoustic method, were excluded during the selection for quantitative analysis. We only included studies published in French or English that measured vulnerability to drought-induced cavitation on stems or branches. For each selected study, we extracted the available information, including species, tree age, sample age, sample conditions, methods used to induce embolism, method used to remove embolism (to determine maximum stem-specific hydraulic conductivity), model used for VC fitting, VC parameter values and their errors, and maximum stem-specific hydraulic conductivity.

Results and discussion

Differences among methods and uncertainty of measurement

There were no differences in the shape of VCs, P₁₂, P₅₀ and P₈₈ between the bench dehydration and pot dehydration methods (Figure 2, Table 1). This result is consistent with the findings reported by Tyree et al. (1992). These methods are not widely used due to their time-consuming nature, resulting in few P₅₀ values determined with these methods in the literature review (Figure 3). However, the shape of the VCs and the associated parameters were remarkedly different for the air injection method, with results that varied greatly among species. For Picea species, stem segments measured with the air injection method were significantly less vulnerable to cavitation, especially regarding P₅₀, than those measured with the bench and pot dehydration methods. This was evident in both our experiment (Figure 2, Table 1) and published literature (significant effect of methods: F_2,65=19.58, P<0.001, Figure 3, Figure 4). P₅₀ values obtained with centrifuge methods were not significantly different from those obtained with air injection methods for P. glauca and P. mariana, but they were significantly less negative for P. abies (significant effect of methods × species interaction: F_5,65=7.96, P<0.001 for the analysis on all species, significant effect of methods: F_2,10=8.66 , P=0.007 for the analysis only on the P. abies data, Figure 3, Figure 4). The VCs of stem segments of P. strobus used for the air injection method showed an ‘exponential' shape (sensu Cochard et al., 2013), indicating a higher vulnerability to cavitation than those measured with the dehydration methods (Figure 2, Table 1). There was little mention of the outcome of the air injection method in the literature for conifer species; artifacts causing ‘exponential' curves are less likely for tracheid-bearing species than for ring-porous species with long vessels. However, Cochard et al. (2013) surveyed a non-negligible amount (c. 15%) of exponential curves built with air injection by the pressure sleeve method for conifer species. These discrepancies could be explained by the different methods used to obtain maximum stem-specific conductivity (Hacke et al., 2015). Some VCs are obtained from stem segments cut from well-hydrated trees (as was the case for both dehydration methods), while others are obtained after infiltrating the stem segment under vacuum (as was the case for the air injection method), or after flushing at low or high pressure (8 to 400 kPa). Although the maximum stem-specific hydraulic conductivity was not significantly different among methods in our experiment (although higher for the air injection method, Table 1), we are conducting further experiments coupled with staining techniques to explore these discrepancies further.

Figure 2 Vulnerability curves constructed using the bench dehydration method (A, D and I), the pot dehydration method (B, E, G and J) and the pressure collar air injection method (C, F, H and K).

Save View full size Expand inline Collapse inline

The percent loss of conductivity (PLC, %) response to decreasing stem water potential MPa for 2-year-old seedlings of (A, B and C) P. glauca, (D, E and F) P. mariana, (G and H) P. abies and (I, J and K) P. strobus. The colored areas represent the confidence interval of the vulnerability curves. For the air injection method, one grey VC represents the VC of a seedling. The vertical solid and dotted lines denote the water potential leading to 50% loss of conductivity (P₅₀) and the confidence interval of the P₅₀, respectively.

Figure 3 Mean values of P50 (-MPa) and their corresponding confidence intervals extracted from published literature on (A) P. glauca, (B) P. mariana, (C) P. abies and (D) P. strobus.

Save View full size Expand inline Collapse inline

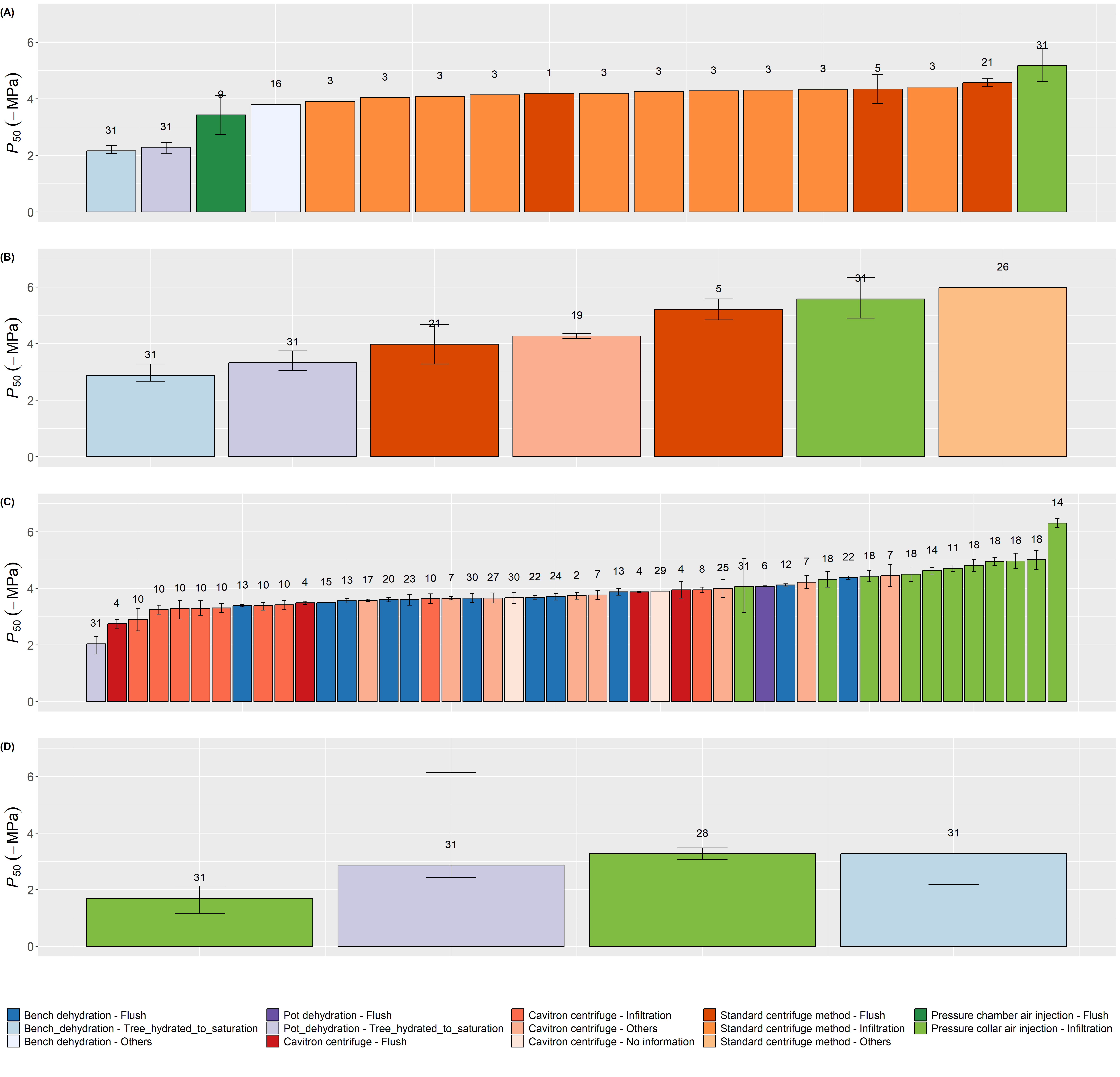
Values are sorted in descending order. Each color represents a different method used to induce embolism where blue denotes bench dehydration, purple denotes pot dehydration, red denotes centrifuge by cavitron method, orange denotes standard centrifuge method, dark green denotes air injection by pressure chamber and light green denotes air injection by pressure collar sleeve chamber. The color luminosity represents the method to remove embolism, where dark denotes flushing, medium denotes infiltration, medium light denotes hydrating trees to saturation, and light denotes no information or others. Numbers indicate unique study identifier (actual study identifier: 31). See Table S1 for reference list.

Figure 4 P50 (-MPa) values extracted from published literature on P. glauca, P. mariana, P. abies and P. strobus for the dehydration, centrifuge and air injection methods used to induce embolism.

Save View full size Expand inline Collapse inline

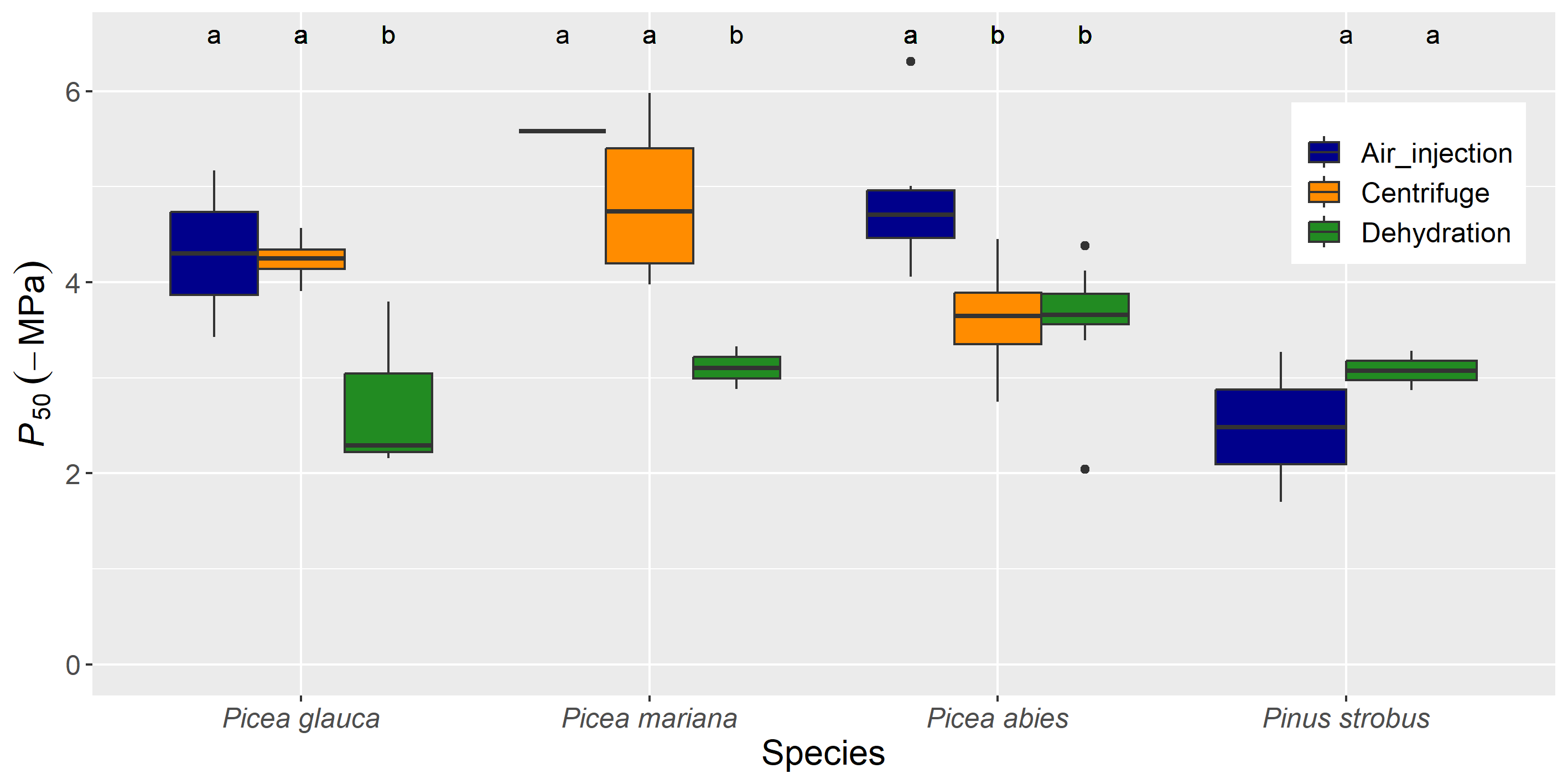
Different letters indicate a significant difference at α < 0.05 between methods for each species.

The observed differences in P₅₀ among various methods for inducing and removing embolism to obtain maximum hydraulic conductivity reveal an uncertainty in the measurements, (i.e., an unexplained variation partially due to measurement error, Lehmann and Rillig, 2014). This uncertainty can be reduced by improving measurement accuracy through the adoption of best practices as recommended in different articles, including the choice of perfusing solution and the driving force, the selection of appropriate sample length and diameter for hydraulic conductivity measurements (Espino and Schenk, 2011; Melcher et al., 2012), the determination of maximum hydraulic conductance (Melcher et al., 2012), and adherence to stability criteria during hydraulic conductivity measurements (De Baerdemaeker et al., 2019). The development of new methods, such as the optical method (Brodribb et al., 2016) and the pneumatic-air-discharge method (Pereira et al., 2016), has made it easier and more cost-effective to construct VCs for a wide range of tracheid and vessel-bearing species, generating more data and a better understanding of embolism propagation in different organs of many species under drought conditions. However, the choice of the appropriate method should also consider the wood anatomy of species, such as vessel- versus tracheid-bearing and ring- versus diffuse-porous species. Several artifacts of measurements were highlighted, particularly for species bearing long vessels (open vessel artifact, Wheeler et al. (2013), Torres-Ruiz et al. (2015), but see also Choat et al. (2010), Sergent et al. (2020), Venturas et al. (2019), and Zhang et al. (2018) for a comparison among VCs constructed for different species using different methods). To ensure consistency, adherence to best practices of different methods (see Paligi et al. (2021) for pneumatic-air-discharge method) should be documented in articles or databases presenting VC measurements as variations in their protocol could be considered as sources of variability inherent to these methods (Figure 5).

Different sources of variability of VCs

Apart from the measurement uncertainty and variability due to the method choice, there could be other sources of variation that could explain the error around the mean curve. While interspecific variability in vulnerability to cavitation is extensively studied (e.g., Maherali et al., 2004; Bartlett et al., 2016), intraspecific variability in this trait is less explored. Studies have shown that intraspecific trait variability (ITV) in vulnerability to cavitation can represent approximately 33% of the interspecific variability within a genus and 20% within a plant functional group (Anderegg, 2015). The ITV of P₅₀ could be attributed to the studied organ, anatomical variation inside a sample, sample age (e.g., Weithmann et al., 2022), tree ontogenetic stage, tree life history (fire, drought, biotic interaction, etc.), and biotic and nutritional environment of trees (see Figure 1 of Anderegg (2015) for a conceptual framework of spatial and temporal variation in vulnerability to cavitation). For instance, anatomical differences between angiosperms and gymnosperms (higher variability of diameter, length, and wall thickness in vessels than in tracheids) could explain the higher ITV in angiosperms compared to gymnosperms (Anderegg, 2015). We thus recommend to include information about plant material such as plant provenance, tree and sample age, tree site, studied organ or tissue at the vessel level, distance from the terminal branch end and maximum vessel length for angiosperms in articles or databases presenting VCs (Figure 5).

Assessing and reporting the variability and the measurement uncertainty of xylem vulnerability curve parameters

Despite the numerous sources of VC variation, they are rarely reported or taken into account in published literature or trait databases (see missing data - absence of error bars - in Figure 3). We argue that VC studies should present the model used for VC fitting with a description of random variation among individual plants when hierarchical models can be used, as with air injection or centrifuge methods. Therefore, the model considers measurement uncertainty of average parameter estimates at the species level (standard error or confidence interval around the mean value of VC parameters) and variability among individuals (standard deviation of the random effect). Some studies presented VCs at the species level built with these methods without considering a random variable or built one VC per individual and presented the VC parameters at the species level as the average of the VC parameters determined at the individual level. In both cases, information regarding the measurement uncertainty and the variability among individuals was lost or biased. The same precautions must be followed in the case of individual-level studies that add branches as random variables. This distinction between uncertainty and variability is not possible for other methods, such as bench and pot dehydration, and both are included in the confidence interval.

Concerning the choice of the model, we recommend using the Weibull function over the exponential-sigmoid function (such as the log-transformed version of Pammenter and Van Der Willigen, 1998), because the Weibull function guarantees that PLC is zero at P=0 (Ogle et al. 2009, Duursma and Choat 2017). We highly recommend the use of the Weibull model as reparametrized by Ogle et al. (2009), as in the fitplc package, which has been increasingly used in recent studies, as the bootstrap CIs (and therefore the determination of asymmetric CIs around the mean value) and the implementation of a hierarchical model are possible. For hierarchical models with a Weibull function, we suggest using the code available in the Supplementary Materials to obtain the confidence intervals around P₁₂ and P₈₈ for the curves fitted with x=50 (because the curve fitting is more robust, Duursma 2018) to avoid fitting three different curves with x defined as 12, 50, and 88 to obtain the CIs of P₁₂, P₅₀, and P₈₈, respectively. Therefore, we suggest properly reporting the model used to fit the VCs (Pammenter and Van Der Willigen (1998), Weibull, or sigmoid) with information about measurement uncertainty (standard error or confidence interval) and variability among individual trees if possible (standard deviation of the estimate of the random effect, as shown in Table 1, or adding the VC of each individual with the mean VC, as shown in Figure 2). These best practices could also be respected for optical or pneumatic-air-discharge methods, as these methods produce VCs with shapes similar to those built using hydraulic methods (Brodribb et al., 2016; Pereira et al., 2016).

We suggest that plant ecophysiologists follow these proposed best practices to improve the assessment and reporting of drought-induced cavitation vulnerability in plants. Knowledge of measurement uncertainty and within-species variability of vulnerability to cavitation can lead to better predictions of tree drought-induced mortality events in plant hydraulic models (Rowland et al., 2021).

Figure 5 Description of best practices for better determining and reporting measurement uncertainty and within-species variability of vulnerability to cavitation.

Save View full size Expand inline Collapse inline

Acknowledgements

We are indebted to Pierre-Nicolas Barbeau, Aurélie Bureau, Megan Byrns, Katherine Galibois, Simon-Pierre Hamel, Marc-Antoine Lambert, Jade Jeantet, Simon Marcouiller, Zachary Sauvageau, Karine Thériault for their help in conducting the experiments. We thank Sylvie Carles for her scientific advice concerning the plant material. We thank Roman Mathias Link and William M. Hammond for their insightful comments during the review process of this manuscript. This work was funded by the Fonds Vert du Québec through a Contrat de recherche forestière obtained from the Ministère des Forêts, de la Faune et des Parcs (Quebec, Canada) by Alison Munson, as part of research project no. 142332161 of the Direction de la recherche forestière (project leader: Catherine Périé).

References

• Adams, H. D., Zeppel, M., Anderegg, W. R. L., Hartmann, H., Landhäusser, S. M., Tissue, D. T., Huxman, T. E., Hudson, P. J., Franz, T. E., Allen, C. D., Anderegg, L. D. L., Barron-Gafford, G. A., Beerling, D. J., Breshears, D. D., Brodribb, T. J., Bugmann, H., Cobb, R. C., Collins, A., Dickman, L. T., . . . McDowell, N. G. (2017). A multi-species synthesis of physiological mechanisms in drought-induced tree mortality. Nature Ecology and Evolution, 1(9), 1285–1291. https://doi.org/10.1038/s41559-017-0248-x
• Anderegg, W. R. L. (2015). Spatial and temporal variation in plant hydraulic traits and their relevance for climate change impacts on vegetation. New Phytologist, 205(3), 1008–1014. https://doi.org/10.1111/nph.12907
• Anderegg, W. R. L., Hicke, J. A., Fisher, R. A., Allen, C. D., Aukema, J. E., Bentz, B., Hood, S. M., Lichstein, J. W., Macalady, A. K., McDowell, N. G., Pan, Y., Raffa, K. F., Sala, A., Shaw, J. D., Stephenson, N. L., Tague, C., & Zeppel, M. (2015). Tree mortality from drought, insects, and their interactions in a changing climate. New Phytologist, 208(3), 674–683. https://doi.org/10.1111/nph.13477
• Anderegg, W. R. L., Klein, T., Bartlett, M. K., Sack, L., Pellegrini, A. F. A., Choat, B., & Jansen, S. (2016). Meta-analysis reveals that hydraulic traits explain cross-species patterns of drought-induced tree mortality across the globe. Proceedings of the National Academy of Sciences of the United States of America, 113(18), 5024–5029. https://doi.org/10.1073/pnas.1525678113
• Aubin, I., Messier, C., Gachet, S., Lawrence, K., McKenney, D., Arseneault, A., Bell, W., De Grandpré, L., Shipley, B., Ricard, J.-P., & Munson, A. D. (2012). TOPIC - Traits of Plants in Canada. Natural Resources Canada, Canadian Forest Service, Sault Ste. Marie, Ontario, Canada. http://www.nrcan.gc.ca/forests/research-centres/glfc/20303
• Bartlett, M. K., Klein, T., Jansen, S., Choat, B., & Sack, L. (2016). The correlations and sequence of plant stomatal, hydraulic, and wilting responses to drought. Proceedings of the National Academy of Sciences, 113(46), 13098–13103. https://doi.org/10.1073/pnas.1604088113
• Boisvert‐Marsh, L., Royer-Tardif, S., Nolet, P., Doyon, F., & Aubin, I. (2020). Using a Trait-Based approach to compare tree species sensitivity to climate change stressors in Eastern Canada and inform adaptation practices. Forests, 11(9), 989. https://doi.org/10.3390/f11090989
• Brodribb, T. J., & Cochard, H. (2009). Hydraulic failure defines the recovery and point of death in Water-Stressed conifers. Plant Physiology, 149(1), 575–584. https://doi.org/10.1104/pp.108.129783
• Brodribb, T. J., Skelton, R. P., McAdam, S. a. M., Bienaimé, D., Lucani, C., & Marmottant, P. (2016). Visual quantification of embolism reveals leaf vulnerability to hydraulic failure. New Phytologist, 209(4), 1403–1409. https://doi.org/10.1111/nph.13846
• Chen, Z., Li, S., Wan, X., & Liu, S. (2022). Strategies of tree species to adapt to drought from leaf stomatal regulation and stem embolism resistance to root properties. Frontiers in Plant Science, 13. https://doi.org/10.3389/fpls.2022.926535
• Choat, B., Brodribb, T. J., Brodersen, C. R., Duursma, R. A., López, R., & Medlyn, B. E. (2018). Triggers of tree mortality under drought. Nature, 558(7711), 531–539. https://doi.org/10.1038/s41586-018-0240-x
• Choat, B., Creek, D., Lo Gullo, M.A., Nardini, A., Oddo, E., Raimondo, F., Torres-Ruiz, J.M., Trifilo, P., Vilagrosa, A. (2015). PrometheusWiki - Quantification of vulnerability to xylem embolism - Bench dehydration. https://www.researchgate.net/publication/282008335_PrometheusWiki_-_Quantification_of_vulnerability_to_xylem_embolism_-_Bench_dehydration
• Choat, B., Drayton, W. M., Brodersen, C. R., Matthews, M. A., Shackel, K. A., Wada, H., & McElrone, A. J. (2010). Measurement of vulnerability to water stress-induced cavitation in grapevine: a comparison of four techniques applied to a long-vesseled species. Plant Cell and Environment, no. https://doi.org/10.1111/j.1365-3040.2010.02160.x
• Choat, B., Jansen, S., Brodribb, T. J., Cochard, H., Delzon, S., Bhaskar, R., Bucci, S., Feild, T. S., Gleason, S. M., Hacke, U. G., Jacobsen, A. L., Lens, F., Maherali, H., Martínez-Vilalta, J., Mayr, S., Mencuccini, M., Mitchell, P., Nardini, A., Pittermann, J., . . . Zanne, A. E. (2012). Global convergence in the vulnerability of forests to drought. Nature, 491(7426), 752–755. https://doi.org/10.1038/nature11688
• Cochard, H., Badel, E., Herbette, S., Delzon, S., Choat, B., & Jansen, S. (2013). Methods for measuring plant vulnerability to cavitation: a critical review. Journal of Experimental Botany, 64(15), 4779–4791. https://doi.org/10.1093/jxb/ert193
• De Baerdemaeker, N. J. F., Arachchige, K. N. R., Zinkernagel, J., Van Den Bulcke, J., Van Acker, J., Schenk, H. J., & Steppe, K. (2019). The stability enigma of hydraulic vulnerability curves: addressing the link between hydraulic conductivity and drought-induced embolism. Tree Physiology, 39(10), 1646–1664. https://doi.org/10.1093/treephys/tpz078
• Delzon, S., & Cochard, H. (2014). Recent advances in tree hydraulics highlight the ecological significance of the hydraulic safety margin. New Phytologist, 203(2), 355–358. https://doi.org/10.1111/nph.12798
• Duursma, R. (2018). Fit Hydraulic Vulnerability curves. https://bitbucket.org/remkoduursma/fitplc/src/master/
• Duursma, R. A., & Choat, B. (2017). fitplc - an R package to fit hydraulic vulnerability curves. Journal of Plant Hydraulics, 4, e002. https://doi.org/10.20870/jph.2017.e002
• Ennajeh, M., Simões, F., Khemira, H., & Cochard, H. (2011). How reliable is the double-ended pressure sleeve technique for assessing xylem vulnerability to cavitation in woody angiosperms? Physiologia Plantarum, 142(3), 205–210. https://doi.org/10.1111/j.1399-3054.2011.01470.x
• Espino, S., & Schenk, H. J. (2011). Mind the bubbles: achieving stable measurements of maximum hydraulic conductivity through woody plant samples. Journal of Experimental Botany, 62(3), 1119–1132. https://doi.org/10.1093/jxb/erq338
• Hacke, U. G., Venturas, M., MacKinnon, E. D., Jacobsen, A. L., Sperry, J. S., & Pratt, R. B. (2015). The standard centrifuge method accurately measures vulnerability curves of long‐vesselled olive stems. New Phytologist, 205(1), 116–127. https://doi.org/10.1111/nph.13017
• Hajek, P., Link, R. M., Nock, C. A., Bauhus, J., Gebauer, T., Gessler, A., Kovach, K., Messier, C., Paquette, A., Saurer, M., Scherer-Lorenzen, M., Rose, L., & Schuldt, B. (2022). Mutually inclusive mechanisms of drought-induced tree mortality. Global Change Biology, 28(10), 3365–3378. https://doi.org/10.1111/gcb.16146
• Hammond, W. P., Yu, K., Wilson, L. A., Will, R. E., Anderegg, W. R. L., & Adams, H. D. (2019). Dead or dying? Quantifying the point of no return from hydraulic failure in drought‐induced tree mortality. New Phytologist, 223(4), 1834–1843. https://doi.org/10.1111/nph.15922
• Jansen, S., Schuldt, B., & Choat, B. (2015). Current controversies and challenges in applying plant hydraulic techniques. New Phytologist, 205(3), 961–964. https://doi.org/10.1111/nph.13229
• Lehmann, J., & Rillig, M. C. (2014). Distinguishing variability from uncertainty. Nature Climate Change, 4(3), 153. https://doi.org/10.1038/nclimate2133
• Lenth, R. (2021). Estimated Marginal Means, aka Least-Squares Means. https://github.com/rvlenth/emmeans
• Liang, X., Ye, Q., Liu, H., & Brodribb, T. J. (2021). Wood density predicts mortality threshold for diverse trees. New Phytologist, 229(6), 3053–3057. https://doi.org/10.1111/nph.17117
• Maherali, H., Pockman, W. T., & Jackson, R. B. (2004). Adaptive Variation in the Vulnerability of Woody Plants to Xylem Cavitation. Ecology, 85(8), 2184–2199. http://www.jstor.org/stable/3450284
• Mantova, M., Menezes-Silva, P. E., Badel, E., Cochard, H., & Torres-Ruiz, J. M. (2021). The interplay of hydraulic failure and cell vitality explains tree capacity to recover from drought. Physiologia Plantarum, 172(1), 247–257. https://doi.org/10.1111/ppl.13331
• Martínez-Vilalta, J., Anderegg, W. R. L., Sapes, G., & Sala, A. (2019). Greater focus on water pools may improve our ability to understand and anticipate drought‐induced mortality in plants. New Phytologist, 223(1), 22–32. https://doi.org/10.1111/nph.15644
• McDowell, N. G., Sapes, G., Pivovaroff, A. L., Adams, H. D., Allen, C. D., Anderegg, W. R. L., Arend, M., Breshears, D. D., Brodribb, T. J., Choat, B., Cochard, H., De Cáceres, M., De Kauwe, M. G., Grossiord, C., Hammond, W. P., Hartmann, H., Hoch, G., Kahmen, A., Klein, T., . . . Xu, C. (2022). Mechanisms of woody-plant mortality under rising drought, CO2 and vapour pressure deficit. Nature Reviews Earth & Environment, 3(5), 294–308. https://doi.org/10.1038/s43017-022-00272-1
• Meinzer, F. C., Johnson, D. M., Lachenbruch, B., McCulloh, K. A., & Woodruff, D. R. (2009). Xylem hydraulic safety margins in woody plants: coordination of stomatal control of xylem tension with hydraulic capacitance. Functional Ecology, 23(5), 922–930. https://doi.org/10.1111/j.1365-2435.2009.01577.x
• Melcher, P. J., Holbrook, N. M., Burns, M. J., Zwieniecki, M. A., Cobb, A. R., Brodribb, T. J., Choat, B., & Sack, L. (2012). Measurements of stem xylem hydraulic conductivity in the laboratory and field. Methods in Ecology and Evolution, 3(4), 685–694. https://doi.org/10.1111/j.2041-210x.2012.00204.x
• Mencuccini, M., Minunno, F., Salmon, Y., Martínez-Vilalta, J., & Hölttä, T. (2015). Coordination of physiological traits involved in drought‐induced mortality of woody plants. New Phytologist, 208(2), 396–409. https://doi.org/10.1111/nph.13461
• Ogle, K., Barber, J. J., Willson, C. J., & Thompson, B. (2009). Hierarchical statistical modeling of xylem vulnerability to cavitation. New Phytologist, 182(2), 541–554. https://doi.org/10.1111/j.1469-8137.2008.02760.x
• Paligi, S., Link, R. M., Isasa, E., Bittencourt, P. R. L., Cabral, J. S., Jansen, S., Oliveira, R. S., Pereira, L., & Schuldt, B. (2021). Accuracy of the pneumatic method for estimating xylem vulnerability to embolism in temperate diffuse-porous tree species. bioRxiv (Cold Spring Harbor Laboratory). https://doi.org/10.1101/2021.02.15.431295
• Pammenter, N. W., & Van Der Willigen, C. (1998). A mathematical and statistical analysis of the curves illustrating vulnerability of xylem to cavitation. Tree Physiology, 18(8–9), 589–593. https://doi.org/10.1093/treephys/18.8-9.589
• Pereira, L., Bittencourt, P. R. L., Oliveira, R. S., Mauro, B. M., Barros, F. V., Ribeiro, R. V., & Mazzafera, P. (2016). Plant pneumatics: stem air flow is related to embolism – new perspectives on methods in plant hydraulics. New Phytologist, 211(1), 357–370. https://doi.org/10.1111/nph.13905
• Pinheiro, J., Bates, D., and R Core Team. (2023). nlme: Linear and Nonlinear Mixed Effects Models. https://CRAN.R-project.org/package=nlme.
• R Core Team. (2020). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.r-project.org/.
• Rowland, L., Martínez-Vilalta, J., & Mencuccini, M. (2021). Hard times for high expectations from hydraulics: predicting drought‐induced forest mortality at landscape scales remains a challenge. New Phytologist, 230(5), 1685–1687. https://doi.org/10.1111/nph.17317
• Sack, L., Bartlett, M.K., Creese, C., Guyot, G., Scoffoni, C., PrometheusWiki contributors. (2011). Constructing and operating a hydraulic flow meter. https://prometheuswiki.rsb.anu.edu.au/tiki-index.php?page=Constructing+and+operating+a+hydraulics+flow+meter
• Schönbeck, L., Schuler, P., Lehmann, M. M., Mas, E., Mekarni, L., Pivovaroff, A. L., Turberg, P., & Grossiord, C. (2022). Increasing temperature and vapour pressure deficit lead to hydraulic damages in the absence of soil drought. Plant Cell and Environment, 45(11), 3275–3289. https://doi.org/10.1111/pce.14425
• Sergent, A., Varela, S., Barigah, T. S., Badel, E., Cochard, H., Dalla-Salda, G., Delzon, S., Fernández, M. E., Guillemot, J., Gyenge, J., Lamarque, L. J., Martinez-Meier, A., Rozenberg, P., Torres-Ruiz, J. M., & Martin-StPaul, N. (2020). A comparison of five methods to assess embolism resistance in trees. Forest Ecology and Management, 468, 118175. https://doi.org/10.1016/j.foreco.2020.118175
• Skelton, R. P., West, A. G., & Dawson, T. E. (2015). Predicting plant vulnerability to drought in biodiverse regions using functional traits. Proceedings of the National Academy of Sciences, 112(18), 5744–5749. https://doi.org/10.1073/pnas.1503376112
• Sperry, J. S., & Tyree, M. T. (1988). Mechanism of water Stress-Induced Xylem embolism. Plant Physiology, 88(3), 581–587. https://doi.org/10.1104/pp.88.3.581
• Stroock, A. D., Pagay, V., Zwieniecki, M. A., & Holbrook, N. M. (2014). The Physicochemical hydrodynamics of vascular plants. Annual Review of Fluid Mechanics, 46(1), 615–642. https://doi.org/10.1146/annurev-fluid-010313-141411
• Torres-Ruiz, J. M., Jansen, S., Choat, B., McElrone, A. J., Cochard, H., Brodribb, T. J., Badel, E., Burlett, R., Bouche, P. S., Brodersen, C. R., Li, S., Morris, H., & Delzon, S. (2015). Direct X-Ray Microtomography Observation Confirms the Induction of Embolism upon Xylem Cutting under Tension. Plant Physiology, 167(1), 40–43. https://doi.org/10.1104/pp.114.249706
• Tyree, M. T., Alexander, J. D., & Machado, J. (1992). Loss of hydraulic conductivity due to water stress in intact juveniles of Quercus rubra and Populus deltoides. Tree Physiology, 10(4), 411–415. https://doi.org/10.1093/treephys/10.4.411
• Urli, M., Porté, A. J., Cochard, H., Guengant, Y., Burlett, R., & Delzon, S. (2013). Xylem embolism threshold for catastrophic hydraulic failure in angiosperm trees. Tree Physiology, 33(7), 672–683. https://doi.org/10.1093/treephys/tpt030
• Venturas, M., Pratt, R. B., Jacobsen, A. L., Castro, V., Fickle, J. C., & Hacke, U. G. (2019). Direct comparison of four methods to construct xylem vulnerability curves: Differences among techniques are linked to vessel network characteristics. Plant Cell and Environment, 42(8), 2422–2436. https://doi.org/10.1111/pce.13565
• Venturas, M., Sperry, J. S., & Hacke, U. G. (2017). Plant xylem hydraulics: What we understand, current research, and future challenges. Journal of Integrative Plant Biology, 59(6), 356–389. https://doi.org/10.1111/jipb.12534
• Venturas, M. D., Todd, H. N., Trugman, A. T., & Anderegg, W. R. L. (2021). Understanding and predicting forest mortality in the western United States using long‐term forest inventory data and modeled hydraulic damage. New Phytologist, 230(5), 1896–1910. https://doi.org/10.1111/nph.17043
• Weithmann, G., Link, R. M., Bat-Enerel, B., Würzberg, L., Leuschner, C., & Schuldt, B. (2022). Soil water availability and branch age explain variability in xylem safety of European beech in Central Europe. Oecologia, 198(3), 629–644. https://doi.org/10.1007/s00442-022-05124-9
• Wheeler, J. K., Huggett, B. A., Tofte, A. N., Rockwell, F. E., & Holbrook, N. M. (2013). Cutting xylem under tension or supersaturated with gas can generate PLC and the appearance of rapid recovery from embolism. Plant Cell and Environment, 36, 1938–1949. https://doi.org/10.1111/pce.12139
• Wubbels J. (2010). Tree species distribution in relation to stem hydraulic traits and soil moisture in a mixed hardwood forest in central Pennsylvania. College of Agricultural Sciences, The Pennsylvania State University. Master thesis. 47pp.
• Zhang, Y., Lamarque, L. J., Torres-Ruiz, J. M., Schuldt, B., Karimi, Z., Li, S., De-Wen, Q., Bittencourt, P. R. L., Burlett, R., Cao, K., Delzon, S., Oliveira, R. S., Pereira, L., & Jansen, S. (2018). Testing the plant pneumatic method to estimate xylem embolism resistance in stems of temperate trees. Tree Physiology, 38(7), 1016–1025. https://doi.org/10.1093/treephys/tpy015